Daily Coding Problems May to Jul
- Daily Coding Problems
- Enviroment Setup
- Jul 31, 2019 LC 240 [Medium] Search a 2D Matrix II
- Jul 30, 2019 LC 74 [Medium] Search a 2D Matrix
- Jul 29, 2019 [Medium] Valid Binary Search Tree
- Jul 28, 2019 LC 169 [Easy] Majority Element
- Jul 27, 2019 [Easy] Map Digits to Letters
- Jul 26, 2019 [Hard] Maximum Number of Applicants
- Additional Question: [Special] Maximum Flow Problem
- Jul 25, 2019 [Medium] Maximum Number of Connected Colors
- Jul 24, 2019 [Medium] Contiguous Sum to K
- Jul 23, 2019 LC 76 [Hard] Minimum Window Substring
- Jul 22, 2019 [Easy] Sorted Square of Integers
- Jul 21, 2019 [Easy] Maximum Subarray Sum
- Jul 20, 2019 [Medium] Cutting a Rod
- Jul 19, 2019 [Medium] Longest Common Subsequence
- Jul 18, 2019 LC 743 [Medium] Network Delay Time
- Jul 17, 2019 LC 312 [Hard] Burst Balloons
- Jul 16, 2019 [Medium] Allocate Minimum Number of Pages
- Jul 15, 2019 [Easy] Fancy Number
- Jul 14, 2019 LT 879 [Medium] NBA Playoff Matches
- Jul 13, 2019 LT 867 [Medium] 4 Keys Keyboard
- Jul 12, 2019 [Medium] Integer Division
- Jul 11, 2019 [Medium] Invert a Binary Tree
- Jul 10, 2019 LT 512 [Medium] Decode Ways
- Jul 9, 2019 LC787 [Medium] Cheapest Flights Within K Stops
- Jul 8, 2019 [Medium] Maximum Path Sum
- Jul 7, 2019 [Easy] Binary Tree Level Sum
- Jul 6, 2019 [Hard] Power Supply to All Cities
- Jul 5, 2019 [Hard] Order of Course Prerequisites
- Additional Question: [Special] Find Cycle in Undirected Graph using Disjoint Set (Union-Find)
- Jul 4, 2019 [Easy] Permutations
- Jul 3, 2019 [Medium] Off-by-One Non-Decreasing Array
- Additional Question: [Special] Longest Path in A Directed Acyclic Graph
- Jul 2, 2019 [Hard] The Longest Increasing Subsequence
- Additional Question: [Special] Strongly Connected Directed Graph
- Jul 1, 2019 [Medium] Merge K Sorted Lists
- June 30, 2019 [Special] Implementing Priority Queue with Heap
- June 29, 2019 [Hard] Largest Sub BST Size
- June 28, 2019 [Special] Stable Marriage Problem
- June 27, 2019 [Medium] Isolated Islands
- June 26, 2019 [Medium] Count Attacking Bishop Pairs
- June 25, 2019 LC 239 [Medium] Sliding Window Maximum
- June 24, 2019 [Medium] E-commerce Website
- June 23, 2019 [Easy] Merge Overlapping Intervals
- June 22, 2019 [Hard] The N Queens Puzzle
- June 21, 2019 [Medium] Invalid Parentheses to Remove
- June 20, 2019 [Medium] Integer Exponentiation
- June 19, 2019 LC 289 [Medium] Conway’s Game of Life
- June 18, 2019 [Medium] Number of Moves on a Grid
- June 17, 2019 [Medium] Multiplication Table
- June 16, 2019 [Easy] N-th Perfect Number
- June 15, 2019 [Hard] Max Path Value in Directed Graph
- June 14, 2019 [Easy] Largest Product of Three
- June 13, 2019 [Medium] Forward DNS Look Up Cache
- June 12, 2019 [Hard] RGB Element Array Swap
- June 11, 2019 [Easy] Word Search Puzzle
- June 10, 2019 [Medium] Locking in Binary Tree
- June 9, 2019 [Medium] Searching in Rotated Array
- June 8, 2019 [Hard] Longest Palindromic Substring
- June 7, 2019 [Medium] K Color Problem
- June 6, 2019 [Medium] Craft Sentence
- June 5, 2019 [Medium] Break Sentence
- June 4, 2019 [Easy] Sell Stock
- June 3, 2019 LC 352 [Hard] Data Stream as Disjoint Intervals
- June 2, 2019 [Hard] Array Shuffle
- June 1, 2019 [Easy] Rand7
- May 31, 2019 [Easy] Rand25, Rand75
- May 30, 2019 [Medium] K-th Missing Number
- May 29, 2019 [Medium] Pre-order & In-order Binary Tree Traversal
- May 28, 2019 [Hard] Subset Sum
- May 27, 2019 [Medium] Multiset Partition
- May 26, 2019 [Medium] Tic-Tac-Toe Game
- May 25, 2019 [Easy] Run-length Encoding
- May 24, 2019 [Medium] Maximum Subarray Sum
- May 23, 2019 [Hard] LRU Cache
- May 22, 2019 [Easy] Special Stack
- May 21, 2019 [Hard] Random Elements from Infinite Stream (Reservoir Sampling)
- May 20, 2019 [Hard] Edit Distance
- May 19, 2019 [Hard] Regular Expression: Period and Asterisk
- May 18, 2019 [Easy] Intersecting Node
- May 17, 2019 LC 332 [Medium] Reconstruct Itinerary
- May 16, 2019 [Easy] Minimum Lecture Rooms
- May 15, 2019 [Medium] Tokenization
- May 14, 2019 [Medium] Overlapping Rectangles
- May 13, 2019 [Medium] Craft Palindrome
- May 12, 2019 [Medium] Inversion Pairs
- May 11, 2019 LC 42 [Hard] Trapping Rain Water
- May 10, 2019 [Hard] Execlusive Product
- May 9, 2019 [Easy] Grid Path
- May 8, 2019 LC 130 [Medium] Surrounded Regions
- May 7, 2019 [Hard] Largest Sum of Non-adjacent Numbers
- May 6, 2019 [Hard] Climb Staircase (Continued)
- May 5, 2019 [Medium] Climb Staircase
- May 4, 2019 [Easy] Power Set
- May 3, 2019 [Easy] Running median of a number stream
- May 2, 2019 [Medium] Remove K-th Last Element from Singly Linked-list
- May 1, 2019 [Easy] Balanced Brackets
- Apr 30, 2019 [Medium] Second Largest in BST
Daily Coding Problems
Enviroment Setup
Python 2.7: https://repl.it/languages/python
Jul 31, 2019 LC 240 [Medium] Search a 2D Matrix II
Question: Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[
[ 1, 4, 7, 11, 15],
[ 2, 5, 8, 12, 19],
[ 3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return True.
Given target = 20, return False.
My thoughts: This problem can be solved using Divide and Conquer. First we find a mid-point (mid of row and column point). We break the matrix into 4 sub-matrices: top-left, top-right, bottom-left, bottom-right. And notice the following properties:
- number in top-left matrix is strictly is less than mid-point
- number in bottom-right matrix is strictly greater than mid-point
- number in the other two could be greater or smaller than mid-point, we cannot say until find out
So each time when we find a mid-point in recursion, if target number is greater than mid-point then we can say that it cannot be in top-left matrix (property 1). So we check all other 3 matrices except top-left.
Or if the target number is smaller than mid-point then we can say it cannot be in bottom-right matrix (property 2). We check all other 3 matrices except bottom-right.
Therefore we have T(mn) = 3/4 * (mn/4) + O(1). By Master Theorem, the time complexity is O(log(mn)) = O(log(m) + log(n))
Solution with Divide and Conquer: https://repl.it/@trsong/Search-a-2D-Matrix-II
import unittest
def search_matrix(matrix, target):
if not matrix or not matrix[0]: return False
n, m = len(matrix), len(matrix[0])
def search_row_col(row, col):
for c in xrange(m):
if matrix[row][c] == target:
return True
for r in xrange(n):
if matrix[r][col] == target:
return True
return False
def search_matrix_recur(rlo, rhi, clo, chi):
if rlo > rhi or clo > chi: return False
rmid = rlo + (rhi - rlo) / 2
cmid = clo + (chi - clo) / 2
if matrix[rmid][cmid] == target:
return True
elif search_row_col(rmid, cmid):
return True
elif matrix[rmid][cmid] > target and search_matrix_recur(rlo, rmid-1, clo, cmid-1):
# target in top left
return True
elif matrix[rmid][cmid] < target and search_matrix_recur(rmid+1, rhi, cmid+1, chi):
# target in bottom right
return True
else:
# target could be in top right or bottom left, we cannot say which is the case
return search_matrix_recur(rlo, rmid-1, cmid+1, chi) or search_matrix_recur(rmid+1, rhi, clo, cmid-1)
return search_matrix_recur(rlo=0, rhi=n-1, clo=0, chi=m-1)
class SearchMatrixSpec(unittest.TestCase):
def test_empty_matrix(self):
self.assertFalse(search_matrix([], target=0))
self.assertFalse(search_matrix([[]], target=0))
def test_example(self):
matrix = [
[ 1, 4, 7,11,15],
[ 2, 5, 8,12,19],
[ 3, 6, 9,16,22],
[10,13,14,17,24],
[18,21,23,26,30]
]
self.assertTrue(search_matrix(matrix, target=5))
self.assertFalse(search_matrix(matrix, target=20))
def test_mid_less_than_top_right(self):
matrix = [
[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9,10],
[11,12,13,14,15],
[16,17,18,19,20],
[21,22,23,24,25]
]
self.assertTrue(search_matrix(matrix, target=5))
def test_mid_greater_than_top_right(self):
matrix = [
[5 , 6,10,14],
[6 ,10,13,18],
[10,13,18,19]
]
self.assertTrue(search_matrix(matrix, target=14))
def test_mid_less_than_bottom_right(self):
matrix = [
[1,4],
[2,5]
]
self.assertTrue(search_matrix(matrix, target=5))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 30, 2019 LC 74 [Medium] Search a 2D Matrix
Question: Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row.
Example 1:
Input:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 3
Output: True
Example 2:
Input:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 13
Output: False
My thoughts: Don’t treat input matrix as array of sorted numbers. Instead, virtually flatten matrix into a long sorted list and perform binary search.
Although the time complexity between performing two binary search vs one is exactly the same. O(log(n) + log(m)) = O(log(nm)).
Solution with Binary Search: https://repl.it/@trsong/Search-a-2D-Matrix
import unittest
def search_matrix(matrix, target):
if not matrix or not matrix[0]: return False
n, m = len(matrix), len(matrix[0])
lo = 0
hi = n * m - 1
while lo <= hi:
mid = lo + (hi - lo) / 2
r, c = mid / m, mid % m
if matrix[r][c] == target:
return True
elif matrix[r][c] < target:
lo = mid + 1
else:
hi = mid - 1
return False
class SearchMatrixSpec(unittest.TestCase):
def setUp(self):
self.matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
def test_empty_matrix(self):
self.assertFalse(search_matrix([], 1))
self.assertFalse(search_matrix([[]], 1))
def test_example(self):
self.assertTrue(search_matrix(self.matrix, target = 3))
self.assertTrue(search_matrix(self.matrix, target = 16))
self.assertFalse(search_matrix(self.matrix, target = 13))
def test_search_boundary_element(self):
self.assertTrue(search_matrix(self.matrix, target = 1))
self.assertTrue(search_matrix(self.matrix, target = 7))
self.assertTrue(search_matrix(self.matrix, target = 23))
self.assertTrue(search_matrix(self.matrix, target = 50))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 29, 2019 [Medium] Valid Binary Search Tree
Question: Determine whether a tree is a valid binary search tree.
A binary search tree is a tree with two children, left and right, and satisfies the constraint that the key in the left child must be less than or equal to the root and the key in the right child must be greater than or equal to the root.
Recursive Solution: https://repl.it/@trsong/Valid-Binary-Search-Tree
import unittest
import sys
class TreeNode(object):
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def is_valid_BST(tree):
def is_valid_BST_recur(tree, low_boundary, hi_boundary):
if not tree: return True
return low_boundary <= tree.val <= hi_boundary and is_valid_BST_recur(tree.left, low_boundary, tree.val) and is_valid_BST_recur(tree.right, tree.val, hi_boundary)
return is_valid_BST_recur(tree, -sys.maxint - 1, sys.maxint)
class IsValidBSTSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertTrue(is_valid_BST(None))
def test_left_tree_invalid(self):
"""
0
/
1
"""
self.assertFalse(is_valid_BST(TreeNode(0, TreeNode(1))))
def test_right_right_invalid(self):
"""
1
/ \
0 0
"""
self.assertFalse(is_valid_BST(TreeNode(1, TreeNode(0), TreeNode(0))))
def test_multi_level_BST(self):
"""
50
/ \
20 60
/ \ / \
5 30 55 70
/ \
65 80
"""
n20 = TreeNode(20, TreeNode(5), TreeNode(30))
n70 = TreeNode(70, TreeNode(65), TreeNode(80))
n60 = TreeNode(60, TreeNode(55), n70)
n50 = TreeNode(50, n20, n60)
self.assertTrue(is_valid_BST(n50))
def test_multi_level_invalid_BST(self):
"""
50
/ \
30 60
/ \ / \
5 20 45 70
/ \
45 80
"""
n30 = TreeNode(30, TreeNode(5), TreeNode(20))
n70 = TreeNode(70, TreeNode(45), TreeNode(80))
n60 = TreeNode(60, TreeNode(45), n70)
n50 = TreeNode(50, n30, n60)
self.assertFalse(is_valid_BST(n50))
if __name__ == '__main__':
unittest.main(exit=False)
Iterative Solution: https://repl.it/@trsong/Valid-Binary-Search-Tree-Iterative
import sys
def is_valid_BST(tree):
stack = [(tree, -sys.maxint - 1, sys.maxint)]
while stack:
cur, low_boundary, hi_boundary = stack.pop()
if not cur:
continue
elif not(low_boundary <= cur.val <= hi_boundary):
return False
else:
stack.append((cur.left, low_boundary, cur.val))
stack.append((cur.right, cur.val, hi_boundary))
return True
Jul 28, 2019 LC 169 [Easy] Majority Element
Question: Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.
You may assume that the array is non-empty and the majority element always exist in the array.
Follow-up: Do that in O(1) Space Complexity.
Example 1:
Input: [3,2,3]
Output: 3
Example 2:
Input: [2,2,1,1,1,2,2]
Output: 2
My thoughts: As this problem requires O(1) space complexity, we cannot use map or priority queue to calculate the count of each element. Instead, besides sort the array and return the n/2’th element, this problem can be solved with divide and conquer: recursively break array into equally left and right parts and let them decide the majority elements separately, after that check if both of them return the same element, otherwise return the element with larger count. And finally, make sure to check the final result to see if it’s really the majority element.
Solution with Divide and Conquer: https://repl.it/@trsong/Majority-Element
import unittest
def majority_element(nums):
n = len(nums)
res = majority_element_recur(nums, 0, n - 1)
count_res = count_range(nums, res, 0, n - 1)
return res if count_res > n / 2 else None
def count_range(nums, target, left, right):
count = 0
for i in xrange(left, right + 1):
if nums[i] == target:
count += 1
return count
def majority_element_recur(nums, left, right):
if left == right:
return nums[left]
mid = left + (right - left) / 2
left_res = majority_element_recur(nums, left, mid)
right_res = majority_element_recur(nums, mid+1, right)
if left_res == right_res:
return left_res
count_left = count_range(nums, left_res, left, mid)
count_right = count_range(nums, right_res, mid+1, right)
return left_res if count_left > count_right else right_res
class MajorityElementSpec(unittest.TestCase):
def test_no_majority_element_exists(self):
self.assertIsNone(majority_element([1, 2, 3, 4]))
def test_example1(self):
self.assertEqual(majority_element([3, 2, 3]), 3)
def test_example2(self):
self.assertEqual(majority_element([2, 2, 1, 1, 1, 2, 2]), 2)
def test_there_is_a_tie(self):
self.assertIsNone(majority_element([1, 2, 1, 2, 1, 2]))
def test_majority_on_second_half_of_list(self):
self.assertEqual(majority_element([2, 2, 1, 2, 1, 1, 1]), 1)
def test_more_than_two_kinds(self):
self.assertEqual(majority_element([1, 2, 1, 1, 2, 2, 1, 3, 1, 1, 1]), 1)
def test_zero_is_the_majority_element(self):
self.assertEqual(majority_element([0, 1, 0, 1, 0, 1, 0]), 0)
if __name__ == '__main__':
unittest.main(exit=False)
Howevever, Boyce-Moore Voting Algorithm is the one we should take a close look at. As it can gives O(n) time complexity and O(1) space complexity: here is how it works, the idea is to shrink the array so that the majority result is equivalent between the original array as well as the shrinked array.
The way we shrink the array is to treat the very first element as majority candidate and shrink the array recursively.
- If the candidate is not majority, there exists an even point p > 0 such that the number of “majority” vs “minority” is the same. And we chop out the array before and equal to the even point p. And the real majority of the rest of array should be the same as the shrinked array
- If the candidate is indeed majority however there is still an even point q such that the number of majority vs minority is the same. And we the same thing to chop out the array before and equal to the even point q. And a majority should still be a majority of the rest of array as we eliminate same number of majority and minority that leaves the majority unchange.
- If the candidate is indeed majority and there is no even point such that the number of majority vs minority is the same. Thus the candidate can be safely returned as majority.
Solution with Boyce-Moore Voting Algorithm: https://repl.it/@trsong/Majority-Element-Boyce-Moore-Algorithms
def majority_element(nums):
n = len(nums)
res = None
count = 0
for elem in nums:
# Treat the first element as candidate for majority elem
# Shrink the array if # of majority candidate equals # of minority elem
if count == 0:
res = elem
count += 1 if elem == res else -1
count_res = count_target(nums, res)
return res if count_res > n / 2 else None
def count_target(nums, target):
count = 0
for elem in nums:
if elem == target:
count += 1
return count
Jul 27, 2019 [Easy] Map Digits to Letters
Question: Given a mapping of digits to letters (as in a phone number), and a digit string, return all possible letters the number could represent. You can assume each valid number in the mapping is a single digit.
For example if {“2”: [“a”, “b”, “c”], 3: [“d”, “e”, “f”], …} then “23” should return [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
My thoughts: The final result equals cartesian product of letters represented by each digit. e.g. "23" = ['a', 'b', 'c'] x ['d', 'e', 'f'] = ['ad', 'ae', 'af', 'bd', 'be', 'bf', 'cd', 'ce', 'cf']
Solution: https://repl.it/@trsong/Map-Digits-to-Letters
import unittest
def cartesian_product(accu_lists, letters):
res = []
for lst in accu_lists:
for l in letters:
res.append(lst[:] + [l])
return res
def digits_to_letters(digits, dictionary):
if not digits: return []
res = [[]]
for digit in digits:
letters = dictionary[digit]
res = cartesian_product(res, letters)
return map(lambda lst: ''.join(lst), res)
class DigitsToLetterSpec(unittest.TestCase):
def assert_letters(self, res, expected):
self.assertEqual(sorted(res), sorted(expected))
def test_empty_digits(self):
self.assert_letters(digits_to_letters("", {}), [])
def test_example(self):
dictionary = {'2': ['a', 'b', 'c'], '3': ['d', 'e', 'f']}
self.assert_letters(
digits_to_letters("23", dictionary),
['ad', 'ae', 'af', 'bd', 'be', 'bf', 'cd', 'ce', 'cf'])
def test_early_google_url(self):
dictionary = {'2': ['a', 'b', 'c'], '3': ['d', 'e', 'f'], '4': ['g', 'h', 'i'], '5': ['j', 'k', 'l'], '6': ['m', 'n', 'o']}
self.assertTrue('google' in digits_to_letters("466453", dictionary))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 26, 2019 [Hard] Maximum Number of Applicants
Question: There are M job applicants and N jobs. Each applicant has a subset of jobs that he/she is interested in. Each job opening can only accept one applicant and a job applicant can be appointed for only one job. Find an assignment of jobs to applicants in such that as many applicants as possible get jobs.
Example:
max_applicants(m=6, n=6, applications=[[1,2], [], [0,3], [2], [2,3],[5]]) # gives 5, as (applicants, jobs) = (0, 1), (2, 0), (3, 2), (4, 3), (5, 5)

My thoughts: Maximum Number of Applicants is a biparte matching problem and can be solved by converting to a max network flow problem. Take a look at Edmonds–Karp Implementation for Ford-Fulkerson Algorithm for details: https://en.wikipedia.org/wiki/Edmonds%E2%80%93Karp_algorithm
Solution with Edmonds–Karp Algorithm: https://repl.it/@trsong/Maximum-Number-of-Applicants
import unittest
def BFS_find_path(neighbor, start, end):
n = len(neighbor)
visited = [False] * n
parent = [-1] * n
queue = [start]
while queue:
cur = queue.pop(0)
if cur == end:
return parent
if not visited[cur]:
visited[cur] = True
for v in neighbor[cur]:
if not visited[v] and neighbor[cur][v] > 0:
parent[v] = cur
queue.append(v)
return None
def max_applicants(num_applicants, num_jobs, applications):
# Create flow graph so that source connects to all applications
# And all jobs connect to sink
neighbor = [None] * (num_applicants + num_jobs + 2)
for applicant in xrange(num_applicants):
jobs = applications[applicant]
neighbor[applicant] = { (num_applicants + job): 1 for job in jobs}
source = -1
sink = -2
neighbor[source] = {applicant: 1 for applicant in xrange(num_applicants)}
for job in xrange(num_jobs):
shifted_job = num_applicants + job
neighbor[shifted_job] = {sink: 1}
max_matching = 0
while True:
path_parent = BFS_find_path(neighbor, source, sink)
if not path_parent:
break
v = sink
while v != source:
u = path_parent[v]
if not neighbor[v]:
neighbor[v] = {}
if u not in neighbor[v]:
neighbor[v][u] = 0
neighbor[u][v] -= 1
neighbor[v][u] += 1
v = u
max_matching += 1
return max_matching
class MaxApplicationSpec(unittest.TestCase):
def test_example(self):
self.assertEqual(max_applicants(num_applicants=6, num_jobs=6, applications=[
[1,2], [], [0,3], [2], [2,3], [5]]), 5)
if __name__ == '__main__':
unittest.main(exit=False)
Additional Question: [Special] Maximum Flow Problem
Question: Given a graph which represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:
1) Flow on an edge doesn’t exceed the given capacity of the edge.
2) Incoming flow is equal to outgoing flow for every vertex except s and t.
For example, consider the following graph from CLRS book.
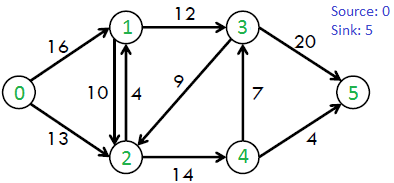
The maximum possible flow in the above graph is 23.
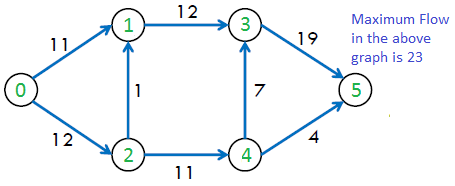
Example:
max_flow(vertices=6, source=0, sink=5, capacity=[
(0, 1, 16), (0, 2, 13), (1, 2, 10), (2, 1, 4),
(1, 3, 12), (3, 2, 9), (2, 4, 14), (4, 3, 7),
(3, 5, 20), (4, 5, 4)]) # returns 23
Note: Implement Ford-Fulkerson Algorithm to solve above problem:
1) Start with initial flow as 0.
2) While there is a augmenting path from source to sink.
Add this path-flow to flow.
3) Return flow.
Take a look at Edmonds–Karp Implementation for Ford-Fulkerson Algorithm for details: https://en.wikipedia.org/wiki/Edmonds%E2%80%93Karp_algorithm
Solution with Edmonds–Karp Algorithm: https://repl.it/@trsong/Maximum-Flow-Problem
import unittest
import sys
def BFS_find_path(neighbor, start, end):
n = len(neighbor)
visited = [False] * n
parent = [-1] * n
queue = [start]
while queue:
cur = queue.pop(0)
if cur == end:
return parent
if not visited[cur]:
visited[cur] = True
for v in neighbor[cur]:
if not visited[v] and neighbor[cur][v] > 0:
parent[v] = cur
queue.append(v)
return None
def max_flow(vertices, source, sink, capacity):
neighbor = [None] * vertices
for u, v, w in capacity:
if not neighbor[u]:
neighbor[u] = {}
neighbor[u][v] = w
max_flow_num = 0
while True:
path_parent = BFS_find_path(neighbor, source, sink)
if not path_parent:
break
# Calculate the bottle-neck of this path and let flow_num be the bottle-neck
flow_num = sys.maxint
v = sink
while v != source:
u = path_parent[v]
flow_num = min(flow_num, neighbor[u][v])
v = u
# All forward edge minus bottle-neck and all backward edge plus bottle-neck
v = sink
while v != source:
u = path_parent[v]
if not neighbor[v]:
neighbor[v] = {}
if u not in neighbor[v]:
neighbor[v][u] = 0
neighbor[u][v] -= flow_num
neighbor[v][u] += flow_num
v = u
max_flow_num += flow_num
return max_flow_num
class MaxFlowSpec(unittest.TestCase):
def test_example(self):
self.assertEqual(max_flow(vertices=6, source=0, sink=5, capacity=[
(0, 1, 16), (0, 2, 13), (1, 2, 10),
(2, 1, 4), (1, 3, 12), (3, 2, 9),
(2, 4, 14), (4, 3, 7), (3, 5, 20), (4, 5, 4)
]), 23)
def test_flow_graph2(self):
self.assertEqual(max_flow(vertices=4, source=0, sink=3, capacity=[
(0, 1, 20), (0, 2, 10), (1, 2, 30), (1, 3, 10), (2, 3, 20)
]), 30)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 25, 2019 [Medium] Maximum Number of Connected Colors
Question: Given a grid with cells in different colors, find the maximum number of same color cells that are connected.
Note: two cells are connected if they are of the same color and adjacent to each other: left, right, top or bottom. To stay simple, we use integers to represent colors:
The following grid have max 4 connected colors. [color 3: (1, 2), (1, 3), (2, 1), (2, 2)]
[
[1, 1, 2, 2, 3],
[1, 2, 3, 3, 1],
[2, 3, 3, 1, 2]
]
My thoughts: Perform BFS/DFS or Union-Find on all unvisited cells, count its neighbors of same color and mark them as visited.
Solution with BFS: https://repl.it/@trsong/Maximum-Number-of-Connected-Colors
import unittest
def max_connected_colors(grid):
n, m = len(grid), len(grid[0])
res = 0
visited = [[False for _ in xrange(m)] for _ in xrange(n)]
for row in xrange(n):
for col in xrange(m):
# Perform BFS on each cell and mark all connected color as visited
if not visited[row][col]:
connected_colors = 0
current_color = grid[row][col]
queue = [(row, col)]
while queue:
level_num = len(queue)
for _ in xrange(level_num):
r, c = queue.pop(0)
if not visited[r][c] and grid[r][c] == current_color:
connected_colors += 1
visited[r][c] = True
if r > 0:
queue.append((r-1, c))
if r < n - 1:
queue.append((r+1, c))
if c > 0:
queue.append((r, c-1))
if c < m - 1:
queue.append((r, c+1))
res = max(res, connected_colors)
return res
class MaxConnectedColorSpec(unittest.TestCase):
def test_empty_graph(self):
self.assertEqual(max_connected_colors([[]]), 0)
def test_example(self):
self.assertEqual(max_connected_colors([
[1, 1, 2, 2, 3],
[1, 2, 3, 3, 1],
[2, 3, 3, 1, 2]
]), 4)
def test_disconnected_colors(self):
self.assertEqual(max_connected_colors([
[1, 0, 1],
[0, 1, 0],
[1, 0, 1]
]), 1)
def test_cross_shap(self):
self.assertEqual(max_connected_colors([
[1, 0, 1],
[0, 0, 0],
[1, 0, 1]
]), 5)
def test_boundary(self):
self.assertEqual(max_connected_colors([
[1, 1, 1],
[1, 0, 1],
[1, 1, 1]
]), 8)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 24, 2019 [Medium] Contiguous Sum to K
Question: Given a list of integers and a number K, return which contiguous elements of the list sum to K.
For example, if the list is
[1, 2, 3, 4, 5]and K is 9, then it should return[2, 3, 4], since 2 + 3 + 4 = 9.
My thoughts: This is a special version of sliding window in a sense that instead of having monotonic increase in [start, end] window. We keep track of all previous [s, end] for all s < end and proceed end.
So the idea of solving this question is to find a specific window [i, j] i.e. j > i such that prefix_sum[j] - prefix_sum[i] = K where prefix_sum[x] is nums[0] + nums[1] + ... + nums[x]. Notice that if nums is non-negative, we can simply use two pointers to keep track of window [i, j]; proceed j if prefix_sum[j] - prefix_sum[i] < K and proceed i if prefix_sum[j] - prefix_sum[i] > K. Such algorithm works for non-negative because prefix_sum[x] only monotonic increase.
However in this question, since we do have negative number as element, we can no longer use two pointers. However, that does not say we cannot have O(n) solution for this problem as we can still calculate prefix_sum[j] - prefix_sum[i] efficiently. Because as we proceed j, we are searching all i < j, that is, we have seen prefix_sum[i] before. And that’s why we have cache come into our place: by keep track of all previous seen prefix_sum[i] for all i < j we can tell whether prefix_sum[j] - prefix_sum[i] = k exists for all i < j which gives the following solution.
Solution with Sliding Window: https://repl.it/@trsong/Contiguous-Sum-to-K
import unittest
def subarray_sum(nums, K):
if not nums: return [] if K == 0 else None
prefix_sum_lookup = {}
sum_so_far = 0
for j in xrange(len(nums)):
sum_so_far += nums[j]
target_sum = sum_so_far - K
if sum_so_far == K:
return nums[0: j+1]
elif target_sum in prefix_sum_lookup:
return nums[prefix_sum_lookup[target_sum]+1: j+1]
else:
prefix_sum_lookup[sum_so_far] = j
return None
class SubarraySumSpec(unittest.TestCase):
def test_empty_array(self):
self.assertEqual(subarray_sum([], 0), [])
self.assertIsNone(subarray_sum([], 1))
def test_non_negative_array(self):
self.assertEqual(subarray_sum([1, 2, 3, 4, 5], 9), [2, 3, 4])
self.assertEqual(subarray_sum([6, 0, 5, 2, 1, 4, 3], 10), [2, 1, 4, 3])
def test_negative_array(self):
self.assertEqual(subarray_sum([-5, -1, -3, -2, -7, -4], -13), [-1, -3, -2, -7])
def test_all_integer_array(self):
self.assertEqual(subarray_sum([1, 2, -1, -2, 4], 0), [1, 2, -1, -2])
self.assertEqual(subarray_sum([1, 2, -3, 7, -1, 4], 5), [2, -3, 7, -1])
self.assertIsNone(subarray_sum([1, 2, -3, 7, -1, 4], 42))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 23, 2019 LC 76 [Hard] Minimum Window Substring
Question: Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).
Note:
If there is no such window in S that covers all characters in T, return the empty string “”.
If there is such window, you are guaranteed that there will always be only one unique minimum window in S.
Example:
Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"
My thoughts: Most substring problem can be solved with Sliding Window method which requires two pointers represent boundaries of a window as well as a map storing certain properties associated w/ letter in substring (in this problem, the count of letter).
In this problem, we first find the count of letter requirement of each letter in target. And we define two pointers: start, end. For each incoming letters, we proceed end and decrease the letter requirement of that letter; once all letter requirement satisfies, we proceed start that will eliminate unnecessary letters to shrink the window size for sure; however it might also introduces new letter requirement and then we proceed end and wait for all letter requirement satisfies again.
We do that over and over and record min window along the way gives the final result.
Solution with Sliding Window: https://repl.it/@trsong/Minimum-Window-Substring
import unittest
import sys
def min_window_substring(source, target):
if not target or len(source) < len(target): return ""
n = len(source)
char_requirement = {}
for c in target:
if c not in char_requirement:
char_requirement[c] = 0
char_requirement[c] += 1
balance = len(target)
start = 0
min_window_size = sys.maxint
min_window_start = 0
for end in xrange(n):
end_char = source[end]
if end_char in char_requirement:
if char_requirement[end_char] > 0:
# char is we want, decrease the balance
balance -= 1
char_requirement[end_char] -= 1
while balance == 0:
# all targt is in the window
if end - start < min_window_size:
min_window_start = start
min_window_size = end - start + 1
start_char = source[start]
if start_char in char_requirement:
if char_requirement[start_char] == 0:
# certain char no longer satisfies requirement
balance += 1
char_requirement[start_char] += 1
start += 1
return "" if min_window_size == sys.maxint else source[min_window_start:min_window_start + min_window_size]
class MinWindowSubstringSpec(unittest.TestCase):
def test_example(self):
source, target, expected = "ADOBECODEBANC", "ABC", "BANC"
self.assertEqual(min_window_substring(source, target), expected)
def test_no_matching_due_to_missing_letters(self):
source, target, expected = "CANADA", "CAB", ""
self.assertEqual(min_window_substring(source, target), expected)
def test_no_matching_due_to_target_too_short(self):
source, target, expected = "USD", "UUSD", ""
self.assertEqual(min_window_substring(source, target), expected)
def test_target_string_with_duplicated_letters(self):
source, target, expected = "BANANAS", "ANANS", "NANAS"
self.assertEqual(min_window_substring(source, target), expected)
def test_matching_window_in_the_middle_of_source(self):
source, target, expected = "AB_AABB_AB_BAB_ABB_BB_BACAB", "ABB", "ABB"
self.assertEqual(min_window_substring(source, target), expected)
def test_matching_window_in_different_order(self):
source, target, expected = "CBADDBBAADBBAAADDDCCBBA", "AAACCCBBBBDDD", "CBADDBBAADBBAAADDDCC"
self.assertEqual(min_window_substring(source, target), expected)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 22, 2019 [Easy] Sorted Square of Integers
Question: Given a sorted list of integers, square the elements and give the output in sorted order.
For example, given
[-9, -2, 0, 2, 3], return[0, 4, 4, 9, 81].Additonal Requirement: Do it in-place. i.e. Space Complexity O(1).
My thoughts: This question requires binary search to find the index of first positive. And then we can rotate negative part of array as it is before the index of first positive. After that we square all numbers. Finally, we will have two sorted array in-place. We will need to merge those two sorted array in-place.
Solution: https://repl.it/@trsong/Sorted-Square-of-Integers
import unittest
def find_positive_index_binary_search(nums):
lo = 0
hi = len(nums)
while lo < hi:
mid = lo + (hi - lo) / 2
if nums[mid] < 0:
lo = mid + 1
else:
hi = mid
return lo
def swap_between(nums, i, j):
while i < j:
nums[i], nums[j] = nums[j], nums[i]
i += 1
j -= 1
def square_between(nums, i, j):
for idx in xrange(i, j+1):
nums[idx] *= nums[idx]
def merge_in_place(nums, s1, s2):
n = len(nums)
while s1 < s2 < n:
while s1 < s2 and nums[s1] <= nums[s2]:
s1 += 1
while s2 < n and nums[s1] > nums[s2]:
tmp = nums[s2]
for i in xrange(s2, s1, -1):
nums[i] = nums[i-1]
nums[s1] = tmp
s1 += 1
s2 += 1
def sorted_square(nums):
positive_start_index = find_positive_index_binary_search(nums)
# If there exists negative number, we flip position of all negative numbers
if positive_start_index > 0:
swap_between(nums, 0, positive_start_index - 1)
# Map all nums into squares
square_between(nums, 0, len(nums) - 1)
# Merge two sorted array in-place
if positive_start_index >= 1:
merge_in_place(nums, 0, positive_start_index)
return nums
class SortedSquareSpec(unittest.TestCase):
def test_array_with_duplicate_elements(self):
self.assertEqual(sorted_square([-1, -1, -1, 0, 0, 0, 1, 1, 1]), [0, 0, 0, 1, 1, 1, 1, 1, 1])
def test_array_with_all_negative_elements(self):
self.assertEqual(sorted_square([-3, -2, -1]), [1, 4, 9])
def test_example(self):
self.assertEqual(sorted_square([-9, -2, 0, 2, 3]), [0, 4, 4, 9, 81])
def test_array_with_positive_elements(self):
self.assertEqual(sorted_square([1, 2, 3]), [1, 4, 9])
def test_array_with_positive_elements(self):
self.assertEqual(sorted_square([-7, -6, 1, 2, 3, 9]), [1, 4, 9, 36, 49, 81])
if __name__ == '__main__':
unittest.main(exit=False)
Jul 21, 2019 [Easy] Maximum Subarray Sum
Question: You are given a one dimensional array that may contain both positive and negative integers, find the sum of contiguous subarray of numbers which has the largest sum.
For example, if the given array is
[-2, -5, 6, -2, -3, 1, 5, -6], then the maximum subarray sum is 7 as sum of[6, -2, -3, 1, 5]equals 7Solve this problem with Divide and Conquer as well as DP separately.
Solution with DP: https://repl.it/@trsong/Maximum-Sub-array-Sum
import unittest
def max_sub_array_sum(nums):
# Let dp[i] represents max sub array sum ends at nums[i-1] inclusive
# Notice dp[i] is only local max sum of subarray with last element as nums[i-1]
# dp[i] = dp[i-1] + nums[i-1] if dp[i-1] > 0
# else = nums[i-1]
n = len(nums)
dp = [0] * (n + 1)
for i in xrange(1, n+1):
dp[i] = nums[i-1] + max(0, dp[i-1])
# The global max sub array is the max of dp,
# i.e. max of all possible maximum of local max of subarray with last element as i
return max(dp)
class MaxSubArraySum(unittest.TestCase):
def test_empty_array(self):
self.assertEqual(max_sub_array_sum([]), 0)
def test_ascending_array(self):
self.assertEqual(max_sub_array_sum([-3, -2, -1, 0, 1, 2, 3]), 6)
def test_descending_array(self):
self.assertEqual(max_sub_array_sum([3, 2, 1, 0, -1]), 6)
def test_example_array(self):
self.assertEqual(max_sub_array_sum([-2, -5, 6, -2, -3, 1, 5, -6]), 7)
def test_negative_array(self):
self.assertEqual(max_sub_array_sum([-2, -1]), 0)
def test_positive_array(self):
self.assertEqual(max_sub_array_sum([1, 2]), 3)
def test_swing_array(self):
self.assertEqual(max_sub_array_sum([-3, 3, -2, 2, -5, 5]), 5)
self.assertEqual(max_sub_array_sum([-1, 1, -1, 1, -1]), 1)
self.assertEqual(max_sub_array_sum([-100, 1, -100, 2, -100]), 2)
def test_converging_array(self):
self.assertEqual(max_sub_array_sum([-3, 3, -2, 2, 1, 0]), 4)
def test_positive_negative_positive_array(self):
self.assertEqual(max_sub_array_sum([7, -1, -2, 3, 1]), 8)
self.assertEqual(max_sub_array_sum([7, -1, -2, 0, 1, 1]), 7)
def test_negative_positive_array(self):
self.assertEqual(max_sub_array_sum([-100, 1, 0, 2, -100]), 3)
if __name__ == '__main__':
unittest.main(exit=False)
Solution with Divide and Conquer: https://repl.it/@trsong/Maximum-Sub-array-Sum-Divide-and-Conquer
def max_sub_array_sum(nums):
if not nums: return 0
return max_sub_array_sum_recur(nums, 0, len(nums) - 1).max
class Result(object):
def __init__(self, x):
self.max = x
self.prefix = x
self.suffix = x
self.sum = x
def max_sub_array_sum_recur(nums, left, right):
if left == right:
return Result(nums[left])
mid = left + (right - left) / 2
left_res = max_sub_array_sum_recur(nums, left, mid)
right_res = max_sub_array_sum_recur(nums, mid+1, right)
res = Result(0)
res.prefix = max(0, left_res.prefix, left_res.sum + right_res.prefix, left_res.sum + right_res.sum)
res.suffix = max(0, right_res.suffix, right_res.sum + left_res.suffix, left_res.sum + right_res.sum)
res.sum = left_res.sum + right_res.sum
res.max = max(res.prefix, res.suffix, left_res.suffix + right_res.prefix, left_res.max, right_res.max)
return res
Jul 20, 2019 [Medium] Cutting a Rod
Question: Given a rod of length n inches and an array of prices that contains prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces.
For example, if length of the rod is 8 and the values of different pieces are given as following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6) = 5 + 17
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 1 5 8 9 10 17 17 20
And if the prices are as following, then the maximum obtainable value is 24 (by cutting in eight pieces of length 1) = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 3 5 8 9 10 17 17 20
My thoughts: Think about the problem backwards: among all rot cutting spaces, at the very last step we have to choose one cut the length n rod into { all (first_rod, second_rod)} = {(0, n), (1, n-1), (2, n-2), ..., (n-1, 1)} And suppose there is a magic function f(n) that can gives the max price we can get when rod length is n, then we can say that f(n) = max of f(first_rod) + price of second_rod for all (first_rod, second_roc), that means, f(n) = max(f(n-k) + price(k)) (index is 1-based) for all k which can be solved using DP.
Solution with DP: https://repl.it/@trsong/Cutting-a-Rod
import unittest
def max_cut_rod_price(piece_prices):
n = len(piece_prices)
# Let dp[i] where 0 <= i <= n represents max cut rod price when the rod length is i
# dp[i] = max(dp[i-k] + piece_prices[k-1]) for k from 1 to i
dp = [0] * (n+1)
for i in xrange(1, n+1):
for k in xrange(1, i+1):
dp[i] = max(dp[i], dp[i-k] + piece_prices[k-1])
return dp[n]
class MaxCutRodPriceSpec(unittest.TestCase):
def test_all_cut_to_one(self):
self.assertEqual(max_cut_rod_price([3, 4, 5]), 9) # 3 + 3 + 3 = 9
def test_cut_to_one_and_two(self):
self.assertEqual(max_cut_rod_price([3, 7, 8]), 10) # 3 + 7 = 10
def test_when_cut_has_tie(self):
self.assertEqual(max_cut_rod_price([1, 3, 4]), 4) # 4 or 1 + 3
def test_no_need_to_cut(self):
self.assertEqual(max_cut_rod_price([1, 2, 5]), 5) # 5
def test_example1(self):
self.assertEqual(max_cut_rod_price([1, 5, 8, 9, 10, 17, 17, 20]), 22) # 5 + 17 = 22
def test_example2(self):
self.assertEqual(max_cut_rod_price([3, 5, 8, 9, 10, 17, 17, 20]), 24) # 3 * 8 = 24
if __name__ == '__main__':
unittest.main(exit=False)
Jul 19, 2019 [Medium] Longest Common Subsequence
Question: Given two sequences, find the length of longest subsequence present in both of them.
A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.
Example 1:
Input: "ABCD" and "EDCA"
Output: 1
Explanation:
LCS is 'A' or 'D' or 'C'
Example 2:
Input: "ABCD" and "EACB"
Output: 2
Explanation:
LCS is "AC"
My thoughts: This problem is similar to Levenshtein Edit Distance in multiple ways:
- If the last digit of each string matches each other, i.e. lcs(seq1 + s, seq2 + s) then result = 1 + lcs(seq1, seq2).
- If the last digit not matches, i.e. lcs(seq1 + s, seq2 + p), then res is either ignore s or ignore q. Just like insert a whitespace or remove a letter from edit distance, which gives max(lcs(seq1, seq2 + p), lcs(seq1 + s, seq2))
The difference between this question and edit distance is that each subsequence does not allow switching to different letters.
Solution with DP: https://repl.it/@trsong/Longest-Common-Sub-sequence
import unittest
def lcs(seq1, seq2):
n, m = len(seq1), len(seq2)
# dp[i][j] represents lcs(seq1[0:i], seq2[0:j]), i from 1 to n, j from 1 to m
# dp[i][j] = 1 + dp[i-1][j-1] if seq1[i-1] match seq2[j-1]
# dp[i][j] = max(dp[i-1][j], dp[i][j-1]) if not match
dp = [[0 for _ in xrange(m+1)] for _ in xrange(n+1)]
for i in xrange(1, n+1):
for j in xrange(1, m+1):
if seq1[i-1] == seq2[j-1]:
dp[i][j] = 1 + dp[i-1][j-1]
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[n][m]
class LCSSpec(unittest.TestCase):
def test_empty_sequences(self):
self.assertEqual(lcs("", ""), 0)
def test_match_last_position(self):
self.assertEqual(lcs("abcdz", "efghijz"), 1) # a
def test_match_first_position(self):
self.assertEqual(lcs("aefgh", "aijklmnop"), 1) # a
def test_off_by_one_position(self):
self.assertEqual(lcs("10101", "01010"), 4) # 0101
self.assertEqual(lcs("12345", "1235"), 4) # 1235
self.assertEqual(lcs("1234", "1243"), 3) # 124
self.assertEqual(lcs("12345", "12340"), 4) # 1234
def test_multiple_matching(self):
self.assertEqual(lcs("afbgchdie", "__a__b_c__de___f_g__h_i___"), 5) # abcde
def test_ascending_vs_descending(self):
self.assertEqual(lcs("01234", "_4__3___2_1_0__"), 1) # 0
def test_multiple_ascending(self):
self.assertEqual(lcs("012312342345", "012345"), 6) # 012345
def test_multiple_descending(self):
self.assertEqual(lcs("5432432321", "54321"), 5) # 54321
def test_example(self):
self.assertEqual(lcs("ABCD", "EACB"), 2) # AC
if __name__ == '__main__':
unittest.main(exit=False)
Jul 18, 2019 LC 743 [Medium] Network Delay Time
Question: There are N network nodes, labelled 1 to N.
Given times, a list of travel times as directed edges
times[i] = (u, v, w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.
Example:
Input: times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
Output: 2
Solution with Dijkstra’s Algorithm: https://repl.it/@trsong/Network-Delay-Time
import unittest
import sys
from Queue import PriorityQueue
def max_network_delay(times, nodes, start):
neighbor = [None] * (nodes + 1)
for u, v, w in times:
if neighbor[u] is None:
neighbor[u] = []
neighbor[u].append((v, w))
# initially set distance to all other nodes to be infinite
distance = [sys.maxint] * (nodes+1)
pq = PriorityQueue()
pq.put((0, start))
while not pq.empty():
dist, node = pq.get()
# If we have previously solved distance for node, then we skip this iteration
if distance[node] < sys.maxint:
continue
distance[node] = dist
if neighbor[node] is None:
continue
for nb, weight in neighbor[node]:
alt = dist + weight
# If neighbor's distance not settle, add alternative path to queue
if distance[nb] == sys.maxint:
pq.put((alt, nb))
distance[0] = 0
max_distance = max(distance)
# if max_distance is infinite that means certain node cannot be reached from start node.
return max_distance if max_distance != sys.maxint else -1
class MaxNetworkDelay(unittest.TestCase):
def test_disconnected_graph(self):
"""
1(start) 3
| |
v v
2 4
"""
times = [[1, 2, 1], [3, 4, 2]]
self.assertEqual(max_network_delay(times, nodes=4, start=1), -1)
def test_unreachable_node(self):
"""
1
|
v
2
|
v
3 (start)
|
v
4
"""
times = [[1, 2, 1], [2, 3, 2], [3, 4, 3]]
self.assertEqual(max_network_delay(times, nodes=4, start=3), -1)
def test_given_example(self):
"""
(start)
2 --> 3
| |
v v
1 4
"""
times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]]
self.assertEqual(max_network_delay(times, nodes=4, start=2), 2)
def test_exist_alternative_path(self):
"""
(start) 1
1 ---> 3
1 | \ 4 | 2
v \ v
2 -> 4
"""
times = [[1, 2, 1], [1, 3, 1], [1, 4, 4], [3, 4, 2]]
self.assertEqual(max_network_delay(times, nodes=4, start=1), 3) # max path: 1 - 3 - 4
def test_graph_with_cycle(self):
"""
(start)
1 --> 2
^ |
| v
4 <-- 3
"""
times = [[1, 2, 1], [2, 3, 1], [3, 4, 1], [4, 1, 1]]
self.assertEqual(max_network_delay(times, nodes=4, start=1), 3) # max path: 1 - 2 - 3
def test_multiple_paths(self):
"""
1 (start)
/|\
/ | \
1| 2| 3|
v v v
2 3 4
2| 3| 1|
v v v
5 6 7
"""
times = [[1, 2, 1], [1, 3, 2], [1, 4, 3], [2, 5, 2], [3, 6, 3], [4, 7, 1]]
self.assertEqual(max_network_delay(times, nodes=7, start=1), 5) # max path: 1 - 3 - 6
if __name__ == '__main__':
unittest.main(exit=False)
Solution with Bellman-Ford Algorithm: https://repl.it/@trsong/Network-Delay-Time-Bellman-Ford
import sys
def max_network_delay(times, nodes, start):
distance = [sys.maxint] * (nodes + 1)
distance[start] = 0
for _ in xrange(nodes-1):
for u, v, w in times:
distance[v] = min(distance[v], distance[u] + w)
distance[0] = 0
res = max(distance)
return res if res != sys.maxint else -1
Jul 17, 2019 LC 312 [Hard] Burst Balloons
Question: Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get
nums[left] * nums[i] * nums[right]coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.Find the maximum coins you can collect by bursting the balloons wisely.
Note:
You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
Example:
Input: [3,1,5,8]
Output: 167
Explanation: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
My thoughts: think about the problem backwards: the last balloon will have coins coins[-1] * coins[i] * coins[n] for some i. We can solve this problem recursively to figure out the index i at each step to give the maximum coins. That gives recursive formula:
burst_in_range_recur(left, right) = max of (coins[left] * coins[i] * coins[right] + burst_in_range_recur(left, i) + burst_in_range_recur(i, right)) for all i between left and right.
The final result is by calling burst_in_range_recur(-1, n).
Solution with DP: https://repl.it/@trsong/Burst-Balloons
import unittest
def burst_balloons(coins):
n = len(coins)
cache = [[None for _ in range(n+2)] for _ in range(n+2)]
return burst_in_range_recur(coins, cache, -1, n)
def burst_in_range_recur(coins, cache, left, right):
if left + 1 >= right:
return 0
elif cache[left][right] is None:
res = 0
left_coins = coins[left] if left >= 0 else 1
right_coins = coins[right] if right < len(coins) else 1
for i in range(left+1, right):
left_res = burst_in_range_recur(coins, cache, left, i)
right_res = burst_in_range_recur(coins, cache, i, right)
res = max(res, left_coins * coins[i] * right_coins + left_res + right_res)
cache[left][right] = res
return cache[left][right]
class BurstBalloonSpec(unittest.TestCase):
def test_sample_example(self):
# Burst 1, 5, 3, 8 in order gives:
# 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
self.assertEqual(burst_balloons([3, 1, 5, 8]), 167)
def test_ascending_balloons(self):
# Burst 3, 2, 1, 4 in order gives:
# 2*3*4 + 1*2*4 + 1*1*4 + 1*4*1 = 40
self.assertEqual(burst_balloons([1, 2, 3, 4]), 40)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 16, 2019 [Medium] Allocate Minimum Number of Pages
Question: Given number of pages in n different books and m students. The books are arranged in ascending order of number of pages. Every student is assigned to read some consecutive books. The task is to assign books in such a way that the maximum number of pages assigned to a student is minimum.
Example:
Input : pages[] = {12, 34, 67, 90}
m = 2
Output : 113
Explanation:
There are 2 number of students. Books can be distributed
in following fashion :
1) [12] and [34, 67, 90]
Max number of pages is allocated to student
2 with 34 + 67 + 90 = 191 pages
2) [12, 34] and [67, 90]
Max number of pages is allocated to student
2 with 67 + 90 = 157 pages
3) [12, 34, 67] and [90]
Max number of pages is allocated to student
1 with 12 + 34 + 67 = 113 pages
Of the 3 cases, Option 3 has the minimum pages = 113.
My thoughts: Think about the problem backwards: let’s first determine how many books the last student can read. He must at least read 1 book and at most n-(s-1) where n is total number of books and s is total number of students as there are s-1 student ahead. We don’t want last student to read too many books, as this would bring up the min number of books a student can read at most. And we dont’t want the last student to read to few books as other student have to read the remaining books and bring up the min number of books a student can read at most.
Thus we see the min of max might come from last student in each iteration or from applying the same algorithm to previous students.
We can solve this problem use DP. Let dp[b][s] represents min of max pages number of s student can read from 0 to b-1 books. dp[b][s] = max(dp[b-i][s-1], sum all pages between b-i to b-1) where i from 1 to b-s+1, here i represent number of book the last student read, and each student at least read 1 book.
Then the dp[n][s] cell will be the min of max book a student can read at most.
Solution with DP: https://repl.it/@trsong/Allocate-Minimum-Number-of-Pages
import unittest
import sys
def allocate_min_num_books(pages, num_students):
n = len(pages)
sum_until = [0] * n
sum_until[0] = pages[0]
for i in xrange(1, n):
sum_until[i] = sum_until[i-1] + pages[i]
def sum_between(i, j):
if i > j:
return 0
elif i > 0:
return sum_until[j] - sum_until[i-1]
else:
return sum_until[j]
# let dp[b][s] represents min of max pages number of s student can read from 0 to b-1 books
# dp[b][s] = max(dp[b-i][s-1], sum all pages between b-i to b-1) where i from 1 to b-s+1,
# here i represent number of book the last student read, and each student at least read 1 book,
dp = [[sys.maxint for _ in xrange(num_students+1)] for _ in xrange(n+1)]
dp[0][0] = 0
for b in xrange(1, n+1):
for s in xrange(1, num_students+1):
for i in xrange(1, b-s+2):
dp[b][s] = min(dp[b][s], max(dp[b-i][s-1], sum_between(b-i, b-1)))
return dp[n][num_students]
class AllocateMinNumBooks(unittest.TestCase):
def test_two_students(self):
pages = [12, 34, 67, 90]
num_students = 2
self.assertEqual(allocate_min_num_books(pages, num_students), 113) # max of book sum([12, 34, 67], [90]) = 12+34+67 = 113
def test_three_students(self):
pages = [1, 1, 1, 1, 1, 1, 1, 1, 1]
num_students = 3
self.assertEqual(allocate_min_num_books(pages, num_students), 3) # max of book sum([1, 1, 1], [1, 1, 1], [1, 1, 1]) = 1+1+1 = 3
def test_four_students(self):
pages = [100, 101, 102, 103, 104]
num_students = 4
self.assertEqual(allocate_min_num_books(pages, num_students), 201) # max of book sum([100, 101], [102], [103], [104]) = 100 + 101 = 201
def test_five_students(self):
pages = [8, 9, 8, 8, 6, 7, 8, 9, 10]
num_students = 5
self.assertEqual(allocate_min_num_books(pages, num_students), 17) # max of book sum([9, 8], [8, 8], [6, 7], [8, 9], [10]) = 9+8 = 17
if __name__ == '__main__':
unittest.main(exit=False)
Jul 15, 2019 [Easy] Fancy Number
Question: Check if a given number is Fancy. A fancy number is one which when rotated 180 degrees is the same. Given a number, find whether it is fancy or not.
180 degree rotations of 6, 9, 1, 0 and 8 are 9, 6, 1, 0 and 8 respectively
Example 1:
Input: num = 96
Output: Yes
If we rotate given number by 180, we get same number
Example 2:
Input: num = 916
Output: Yes
If we rotate given number by 180, we get same number
Example 3:
Input: num = 996
Output: No
Example 4:
Input: num = 121
Output: No
Solution: https://repl.it/@trsong/Fancy-Number
import unittest
rotation_mapping = [0, 1, None, None, None, None, 9, None, 8, 6]
def reverse_rotate(num):
global rotation_mapping
reverse_rotation_res = 0
while num > 0:
rotation = rotation_mapping[num % 10]
if rotation is None: return None
reverse_rotation_res = 10 * reverse_rotation_res + rotation
num /= 10
return reverse_rotation_res
def is_fancy_number(num):
return num == reverse_rotate(num)
class IsFancyNumberSpec(unittest.TestCase):
def test_fancy_number(self):
self.assertTrue(is_fancy_number(69))
self.assertTrue(is_fancy_number(916))
self.assertTrue(is_fancy_number(0))
def test_not_fancy_number(self):
self.assertFalse(is_fancy_number(996))
self.assertFalse(is_fancy_number(121))
self.assertFalse(is_fancy_number(110))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 14, 2019 LT 879 [Medium] NBA Playoff Matches
Question: During the NBA playoffs, we always arrange the rather strong team to play with the rather weak team, like make the rank 1 team play with the rank nth team, which is a good strategy to make the contest more interesting. Now, you’re given n teams, and you need to output their final contest matches in the form of a string.
The n teams are given in the form of positive integers from 1 to n, which represents their initial rank. (Rank 1 is the strongest team and Rank n is the weakest team.) We’ll use parentheses () and commas , to represent the contest team pairing - parentheses () for pairing and commas , for partition. During the pairing process in each round, you always need to follow the strategy of making the rather strong one pair with the rather weak one.
We ensure that the input n can be converted into the form
2^k, where k is a positive integer.
Example 1:
Input: 2
Output: "(1,2)"
Example 2:
Input: 4
Output: "((1,4),(2,3))"
Explanation:
In the first round, we pair the team 1 and 4, the team 2 and 3 together, as we need to make the strong team and weak team together.
And we got (1,4),(2,3).
In the second round, the winners of (1,4) and (2,3) need to play again to generate the final winner, so you need to add the paratheses outside them.
And we got the final answer ((1,4),(2,3)).
Example 3:
Input: 8
Output: "(((1,8),(4,5)),((2,7),(3,6)))"
Explanation:
First round: (1,8),(2,7),(3,6),(4,5)
Second round: ((1,8),(4,5)),((2,7),(3,6))
Third round: (((1,8),(4,5)),((2,7),(3,6)))
Solution: https://repl.it/@trsong/NBA-Playoff-Matches
import unittest
def NBA_Playoff_Matches(n):
res = [[str(x)] for x in xrange(1, n+1)]
while n > 0:
for i in xrange(n/2):
# Per round, match highest-rank team with lowest-rank team
res[i] = ["("] + res[i] + [","] + res[n-1-i] + [")"]
n = n / 2
return "".join(res[0])
class NBAPlayoffMatcheSpec(unittest.TestCase):
def test_2_teams(self):
self.assertEqual(NBA_Playoff_Matches(2), "(1,2)")
def test_4_teams(self):
self.assertEqual(NBA_Playoff_Matches(4), "((1,4),(2,3))")
def test_8_teams(self):
self.assertEqual(NBA_Playoff_Matches(8), "(((1,8),(4,5)),((2,7),(3,6)))")
if __name__ == '__main__':
unittest.main(exit=False)
Jul 13, 2019 LT 867 [Medium] 4 Keys Keyboard
Question: Imagine you have a special keyboard with the following keys:
Key 1: (A): Print one 'A' on screen.
Key 2: (Ctrl-A): Select the whole screen.
Key 3: (Ctrl-C): Copy selection to buffer.
Key 4: (Ctrl-V): Print buffer on screen appending it after what has already been printed.
Now, you can only press the keyboard for N times (with the above four keys), find out the maximum numbers of ‘A’ you can print on screen.
Example 1:
Input: 3
Output: 3
Explanation: A, A, A
Example 2:
Input: 7
Output: 9
Explanation: A, A, A, Ctrl A, Ctrl C, Ctrl V, Ctrl V
My thoughts: This question can be solved with DP. Let dp[n] to be the max number of A’s when the problem size is n. Then we want to define sub-problems and combine result of subproblems:
First, notice that when max number of A’s equals n when n <= 6. Second, if n > 6, we want to accumulate enought A’s before we can double the result. Thus the last few keys must all be Ctrl + V. But we also see that the overhead of double the total number of A’s is 3: we need Ctrl + A, Ctrl + C and Ctrl + V to double the size of n - 3 problem. And we can do Ctrl + V and another Ctrl + V back-to-back to bring two copys of original string. That will triple the number of A’s of n - 4 problem.
Thus based on above observation, we find that the recursive formula is dp[n] = max(2 * dp[n-3], 3 * dp[n - 4], 4 * dp[n - 5], ..., (k-1) * dp[n-k], ..., (n-2) * dp[1]). As for certain problem size k, it is calculated over and over again, we will need to cache the result.
Top-down DP Solution: https://repl.it/@trsong/4-Keys-Keyboard
import unittest
def solve_four_keys_keyboard_helper(n, cache):
if n <= 6: return n
max_keys = 0
for k in xrange(3, n):
sub_problem = solve_four_keys_keyboard_with_cache(n - k, cache)
num_copy = k - 2 + 1 # take out Ctrl + A, Ctrl + C and plus one for original copy
max_keys = max(max_keys, num_copy * sub_problem)
return max_keys
def solve_four_keys_keyboard_with_cache(n, cache):
if cache[n] is None:
cache[n] = solve_four_keys_keyboard_helper(n, cache)
return cache[n]
def solve_four_keys_keyboard(n):
cache = [None] * (n + 1)
return solve_four_keys_keyboard_with_cache(n, cache)
class SolveFourKeysKeyboardSpec(unittest.TestCase):
def test_n_less_than_7(self):
self.assertEqual(solve_four_keys_keyboard(0), 0)
self.assertEqual(solve_four_keys_keyboard(1), 1) # A
self.assertEqual(solve_four_keys_keyboard(2), 2) # A, A
self.assertEqual(solve_four_keys_keyboard(3), 3) # A, A, A
self.assertEqual(solve_four_keys_keyboard(4), 4) # A, A, A, A
self.assertEqual(solve_four_keys_keyboard(5), 5) # A, A, A, A, A
self.assertEqual(solve_four_keys_keyboard(6), 6) # A, A, A, Ctrl + A, Ctrl + C, Ctrl + V
def test_n_greater_than_7(self):
self.assertEqual(solve_four_keys_keyboard(7), 9) # A, A, A, Ctrl + A, Ctrl + C, Ctrl + V, Ctrl + V
self.assertEqual(solve_four_keys_keyboard(8), 12) # A, A, A, A, Ctrl + A, Ctrl + C, Ctrl + V, Ctrl + V
if __name__ == '__main__':
unittest.main(exit=False)
Jul 12, 2019 [Medium] Integer Division
Question: Implement division of two positive integers without using the division, multiplication, or modulus operators. Return the quotient as an integer, ignoring the remainder.
My thoughts: The quotient can be broken down into sum of multiple 2’s powers. e.g. 321 = 45 * 7 + 6 = (32 + 8 + 4 + 1) * 7 + 6. Thus we can sums up those 2’s powers to get quotient.
Solution: https://repl.it/@trsong/Integer-Division
import unittest
def divide(dividend, divisor):
if divisor == 0: raise ZeroDivisionError
sign = -1 if (dividend > 0) ^ (divisor > 0) else 1
abs_dividend = abs(dividend)
abs_divisor = abs(divisor)
quotient = 0
while abs_dividend > abs_divisor:
base = 0
while abs_dividend - (abs_divisor << (base + 1)) >= 0:
base += 1
abs_dividend -= abs_divisor << base
quotient += 1 << base
if sign * abs_dividend < 0 and dividend < 0:
return sign * quotient - 1
else:
return sign * quotient
class DivideSpec(unittest.TestCase):
def test_divide_by_zero(self):
self.assertRaises(ZeroDivisionError, divide, 1, 0)
def test_dividend_is_divisible(self):
self.assertEqual(divide(30, 5), 6)
self.assertEqual(divide(0, 5), 0)
def test_dividend_is_negative(self):
self.assertEqual(divide(-25, 7), -4)
self.assertEqual(divide(-18, 3), -6)
def test_dividend_is_positive(self):
self.assertEqual(divide(321, 7), 45)
self.assertEqual(divide(123, 455), 0)
def test_divisor_is_negative(self):
self.assertEqual(divide(43, -8), -5)
def test_both_numbers_are_negative(self):
self.assertEqual(divide(-10, -3), 3)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 11, 2019 [Medium] Invert a Binary Tree
Question: Invert a binary tree.
For example, given the following tree:
a
/ \
b c
/ \ /
d e f
should become:
a
/ \
c b
\ / \
f e d
Solution: https://repl.it/@trsong/Invert-a-Binary-Tree
import unittest
class TreeNode(object):
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def __eq__(self, other):
return other is not None and other.val == self.val and other.left == self.left and other.right == self.right
def invert_tree(tree):
if not tree: return None
tree.left, tree.right = invert_tree(tree.right), invert_tree(tree.left)
return tree
class InvertTreeSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertIsNone(invert_tree(None))
def test_heavy_left_tree(self):
"""
1
/
2
/
3
"""
tree = TreeNode(1, TreeNode(2, TreeNode(3)))
"""
1
\
2
\
3
"""
expected_tree = TreeNode(1, right=TreeNode(2, right=TreeNode(3)))
self.assertEqual(invert_tree(tree), expected_tree)
def test_heavy_right_tree(self):
"""
1
/ \
2 3
/
4
"""
tree = TreeNode(1, TreeNode(2), TreeNode(3, TreeNode(4)))
"""
1
/ \
3 2
\
4
"""
expected_tree = TreeNode(1, TreeNode(3, right=TreeNode(4)), TreeNode(2))
self.assertEqual(invert_tree(tree), expected_tree)
def test_sample_tree(self):
"""
1
/ \
2 3
/ \ /
4 5 6
"""
n2 = TreeNode(2, TreeNode(4), TreeNode(5))
n3 = TreeNode(3, TreeNode(6))
n1 = TreeNode(1, n2, n3)
"""
1
/ \
3 2
\ / \
6 5 4
"""
en2 = TreeNode(2, TreeNode(5), TreeNode(4))
en3 = TreeNode(3, right=TreeNode(6))
en1 = TreeNode(1, en3, en2)
self.assertEqual(invert_tree(n1), en1)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 10, 2019 LT 512 [Medium] Decode Ways
Question: A message containing letters from A-Z is being encoded to numbers using the following mapping: ‘A’ -> 1 ‘B’ -> 2 … ‘Z’ -> 26 Given an encoded message containing digits, determine the total number of ways to decode it.
Example 1:
Input: "12"
Output: 2
Explanation: It could be decoded as AB (1 2) or L (12).
Example 2:
Input: "10"
Output: 1
My thoughts: This question can be solved w/ DP. Similar to the climb stair problem, DP[n] = DP[n-1] + DP[n-2] under certain conditions. If last digits can form a number, i.e. 1-9 then DP[n] = DP[n-1]. And if last two digits can form a number, i.e. 10 - 26, then DP[n] = DP[n-2]. If we consider both digits, we will have
dp[k] = dp[k-1] if str[k-1] can form a number. i.e not zero, 1-9
+ dp[k-2] if str[k-2] and str[k-1] can form a number. 10-26
Solution with DP: https://repl.it/@trsong/Decode-Ways
import unittest
def decode_ways(encoded_string):
# Let dp[n] represent the number of way to decode when the input size = n
# dp[1] = 1
# dp[k] = dp[k-1] if str[k-1] can form a number. i.e not zero, 1-9
# + dp[k-2] if str[k-2] and str[k-1] can form a number. 10-26
n = len(encoded_string)
dp = [0] * (n + 1)
dp[0] = 1
dp[1] = 1
ord_0 = ord('0')
for i in xrange(2, n+1):
last_digit = ord(encoded_string[i-1]) - ord_0
second_last_digit = ord(encoded_string[i-2]) - ord_0
if last_digit > 0:
dp[i] += dp[i-1]
if 10 <= 10 * second_last_digit + last_digit <= 26:
dp[i] += dp[i-2]
return dp[n]
class DecodeWaySpec(unittest.TestCase):
def test_length_one_string(self):
self.assertEqual(decode_ways("2"), 1)
self.assertEqual(decode_ways("9"), 1)
def test_length_two_string(self):
self.assertEqual(decode_ways("20"), 1) # 20
self.assertEqual(decode_ways("19"), 2) # 1,9 and 19
def test_length_three_string(self):
self.assertEqual(decode_ways("121"), 3) # 1, 20 and 12, 0
self.assertEqual(decode_ways("120"), 1) # 1, 20
self.assertEqual(decode_ways("209"), 1) # 20, 9
self.assertEqual(decode_ways("912"), 2) # 9,1,2 and 9,12
self.assertEqual(decode_ways("231"), 2) # 2,3,1 and 23, 1
self.assertEqual(decode_ways("123"), 3) # 1,2,3, and 1, 23 and 12, 3
def test_length_four_string(self):
self.assertEqual(decode_ways("1234"), 3)
self.assertEqual(decode_ways("1111"), 5)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 9, 2019 LC787 [Medium] Cheapest Flights Within K Stops
Question: There are
ncities connected bymflights. Each fight starts from cityuand arrives atvwith a pricew.Now given all the cities and flights, together with starting city
srcand the destinationdst, your task is to find the cheapest price fromsrctodstwith up tokstops. If there is no such route, output-1.
Example 1:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Example 2:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
My thoguhts: Initially I thought this problem can be solved by pre-processing the graph with BFS to eliminate certain vertices and edges within range K and then perform original Dijkstra’s Algorithm. However I encountered a counter-example: [(0, 1, 100), (1, 2, 100), (2, 3, 100), (0, 2, 500)] with src = 0, dst = 3 and K = 1. You can see that none of edge and vertex can be eliminated. But the final result is 500 other than 300.
The correct way to solve the problem is to allow Dijstra’s Algorithm to be able to store path-length during the traversal of the graph. If number of path-length exceed the limit (defined as number of stops a flight can take), we never allow that vertex to exist in the priority queue. And the priority of vertex is depended on accumulated cost so that each vertex might exist in the queue mutltiple times with different accumulated cost as well as remaining path length. As the priority queue is implemented by a min-heap, we are guaranteed that for each vertex, we always return the lowest accumulated cost one for a specific vertex.
Note: as the shortest path without number of stops constraint might not satisfy the requirement, any path could satisfy the shortest path with constraint. Thus there is not need to keep track of lowest cost array defined in original Dijkstra’s Algorithm.
Solution with Modified Dijkstra’s Algorithm: https://repl.it/@trsong/Cheapest-Flights-Within-K-Stops
import unittest
from queue import PriorityQueue
def findCheapestPrice(n, flights, src, dst, K):
max_path_length = K + 1
neighbor = { v: {} for v in xrange(n) }
for edge in flights:
u, v, w = edge
neighbor[u][v] = w
pq = PriorityQueue()
pq.put((0, src, max_path_length))
while not pq.empty():
accumulated_cost, airport, path_length = pq.get()
if airport == dst:
return accumulated_cost
elif path_length > 0:
for nb in neighbor[airport]:
pq.put((accumulated_cost + neighbor[airport][nb], nb, path_length - 1))
return -1
class FindCheapestPriceSpec(unittest.TestCase):
def test_lowest_price_yet_unqualified_stops(self):
self.assertEqual(findCheapestPrice(3, [(0, 1, 100), (1, 2, 100), (0, 2, 300)], 0, 2, 0), 300)
def test_lowest_price_with_qualified_stops(self):
self.assertEqual(findCheapestPrice(3, [(0, 1, 100), (1, 2, 100), (0, 2, 300)], 0, 2, 1), 200)
def test_cheap_yet_more_stops(self):
flights = [(0, 1, 100), (1, 2, 100), (2, 3, 100), (0, 2, 500)]
self.assertEqual(findCheapestPrice(4, flights, 0, 3, 0), -1)
self.assertEqual(findCheapestPrice(4, flights, 0, 3, 1), 600)
self.assertEqual(findCheapestPrice(4, flights, 0, 3, 2), 300)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 8, 2019 [Medium] Maximum Path Sum
Question: Given a binary tree of integers, find the maximum path sum between two nodes. The path must go through at least one node, and does not need to go through the root.
My thoughts: The maximum path sum can either inherit from maximum of recursive children value or calculate based on maximum left path sum and right path sum.
Example1: Final result inherits from children
0
/ \
2 0
/ \ /
4 5 0
Example2: Final result is calculated based on max left path sum and right path sum
1
/ \
2 3
/ / \
8 0 5
/ \ \
0 0 9
Solution: https://repl.it/@trsong/Maximum-Path-Sum
import unittest
class TreeNode(object):
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def max_path_sum(tree):
def max_path_sum_helper(tree):
if not tree: return 0, 0
lps, max_lps = max_path_sum_helper(tree.left)
rps, max_rps = max_path_sum_helper(tree.right)
# Maintain longest path sum from left and right child
cur_ps = tree.val + max(lps, rps)
max_cur_ps = tree.val + lps + rps
max_child_ps = max(max_lps, max_rps)
# The max path sum comes from:
# - either inheritance from children
# - or calculate based on sum of left longest path sum, right longest path sum, and current value
return cur_ps, max(max_cur_ps, max_child_ps)
return max_path_sum_helper(tree)[1]
class MaxPathSumSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertEqual(max_path_sum(None), 0)
def test_max_path_sum_not_pass_root(self):
"""
1
/ \
2 0
/ \ /
4 5 1
"""
n2 = TreeNode(2, TreeNode(4), TreeNode(5))
n0 = TreeNode(0, TreeNode(1))
root = TreeNode(1, n2, n0)
self.assertEqual(max_path_sum(root), 11) # Path: 4 - 2 - 5
def test_max_path_sum_pass_root(self):
"""
1
/
2
/
3
/
4
"""
n3 = TreeNode(3, TreeNode(4))
n2 = TreeNode(2, n3)
n1 = TreeNode(1, n2)
self.assertEqual(max_path_sum(n1), 10) # Path: 1 - 2 - 3 - 4
def test_heavy_right_tree(self):
"""
1
/ \
2 3
/ / \
8 4 5
/ \ \
6 7 9
"""
n5 = TreeNode(5, right=TreeNode(9))
n4 = TreeNode(4, TreeNode(6), TreeNode(7))
n3 = TreeNode(3, n4, n5)
n2 = TreeNode(2, TreeNode(8))
n1 = TreeNode(1, n2, n3)
self.assertEqual(max_path_sum(n1), 28) # Path: 8 - 2 - 1 - 3 - 5 - 9
if __name__ == '__main__':
unittest.main(exit=False)
Jul 7, 2019 [Easy] Binary Tree Level Sum
Question: Given a binary tree and an integer which is the depth of the target level. Calculate the sum of the nodes in the target level.
Solution with BFS: https://repl.it/@trsong/Binary-Tree-Level-Sum
import unittest
class TreeNode(object):
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def tree_level_sum(tree, level):
queue = [tree]
depth_so_far = 0
level_sum = 0
while queue and depth_so_far <= level:
level_size = len(queue)
for _ in xrange(level_size):
current = queue.pop(0)
if current:
queue.append(current.left)
queue.append(current.right)
if depth_so_far == level:
level_sum += current.val
depth_so_far += 1
return level_sum
class TreeLevelSumSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertEqual(tree_level_sum(None, 0), 0)
self.assertEqual(tree_level_sum(None, 1), 0)
def test_complete_tree(self):
"""
1
/ \
2 3
/ \ /
4 5 6
"""
n2 = TreeNode(2, TreeNode(4), TreeNode(5))
n3 = TreeNode(3, TreeNode(6))
n1 = TreeNode(1, n2, n3)
self.assertEqual(tree_level_sum(n1, 2), 15)
self.assertEqual(tree_level_sum(n1, 0), 1)
def test_heavy_left_tree(self):
"""
1
/
2
/
3
/
4
"""
n3 = TreeNode(3, TreeNode(4))
n2 = TreeNode(2, n3)
n1 = TreeNode(1, n2)
self.assertEqual(tree_level_sum(n1, 0), 1)
self.assertEqual(tree_level_sum(n1, 3), 4)
def test_heavy_right_tree(self):
"""
1
/ \
2 3
/ / \
8 4 5
/ \ \
6 7 9
"""
n5 = TreeNode(5, right=TreeNode(9))
n4 = TreeNode(4, TreeNode(6), TreeNode(7))
n3 = TreeNode(3, n4, n5)
n2 = TreeNode(2, TreeNode(8))
n1 = TreeNode(1, n2, n3)
self.assertEqual(tree_level_sum(n1, 0), 1)
self.assertEqual(tree_level_sum(n1, 1), 5)
self.assertEqual(tree_level_sum(n1, 2), 17)
self.assertEqual(tree_level_sum(n1, 3), 22)
self.assertEqual(tree_level_sum(n1, 4), 0)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 6, 2019 [Hard] Power Supply to All Cities
Question: Given a graph of possible electricity connections (each with their own cost) between cities in an area, find the cheapest way to supply power to all cities in the area.
My thoughts: This question is an undirected graph problem asking for minimum spanning tree. And there are two algorithms to solve this problem: Kruskal’s vs Prim’s MST Algorithm. First one keeps choosing edges whereas second one starts from connecting vertices. Either one shall work. However, personally I prefer Kruskal’s MST Algorithm, as you can see how easy it is to implement using Python.
Solution with Kruskal’s MST Algorithm: https://repl.it/@trsong/Power-Supply-to-All-Cities
import unittest
class DisjointSet(object):
def __init__(self, arr):
self._parent = { e: e for e in arr }
def find(self, e):
while self._parent[e] != e:
e = self._parent[e]
return e
def union(self, e1, e2):
parent1 = self.find(e1)
parent2 = self.find(e2)
if parent1 != parent2:
self._parent[parent1] = parent2
def is_connected(self, e1, e2):
return self.find(e1) == self.find(e2)
def min_cost_power_supply(cities, cost_btw_cities):
uf = DisjointSet(cities)
connections_order_by_cost = sorted(cost_btw_cities, key=lambda connection: connection[-1])
chosen_connections = []
for connection in connections_order_by_cost:
src, dst, _ = connection
if not uf.is_connected(src, dst):
chosen_connections.append((src, dst))
uf.union(src, dst)
return chosen_connections
class MinCostPowerSupplySpec(unittest.TestCase):
def generate_cost_lookup(self, cities, cost_btw_cities):
cost_lookup = { city: {} for city in cities }
for connection in cost_btw_cities:
src, dst, cost = connection
cost_lookup[src][dst] = cost
cost_lookup[dst][src] = cost
return cost_lookup
def assert_power_supply_cost(self, cities, cost_btw_cities, expected_cost):
"""Test utility to validate the minimum spanning tree result"""
chosen_connections = min_cost_power_supply(cities, cost_btw_cities)
# Make sure it's a tree. A tree has n - 1 edges.
self.assertEqual(len(chosen_connections), len(cities) - 1)
# Make sure it's a spanning tree: a tree that covers all vertices
chosen_cities = set()
for connection in chosen_connections:
chosen_cities.add(connection[0])
chosen_cities.add(connection[1])
self.assertEqual(set(cities), chosen_cities)
# Make sure the cost satisfies the expected
total_cost = 0
cost_lookup = self.generate_cost_lookup(cities, cost_btw_cities)
for connection in chosen_connections:
src, dst = connection
total_cost += cost_lookup[src][dst]
self.assertEqual(total_cost, expected_cost)
def test_k3_graph(self):
cities = ['Vancouver', 'Richmond', 'Burnaby']
cost_btw_cities = [
('Vancouver', 'Richmond', 1),
('Vancouver', 'Burnaby', 1),
('Richmond', 'Burnaby', 2)
]
self.assert_power_supply_cost(cities, cost_btw_cities, 2) # (Vancouver, Burnaby), (Vancouver, Richmond)
def test_k4_graph(self):
cities = ['Toronto', 'Mississauga', 'Waterloo', 'Hamilton']
cost_btw_cities = [
('Mississauga', 'Toronto', 1),
('Toronto', 'Waterloo', 2),
('Waterloo', 'Hamilton', 3),
('Toronto', 'Hamilton', 2),
('Mississauga', 'Hamilton', 1),
('Mississauga', 'Waterloo', 2)
]
self.assert_power_supply_cost(cities, cost_btw_cities, 4) # (Toronto, Mississauga), (Toronto, Waterloo), (Mississauga, Hamilton)
def test_connected_graph(self):
cities = ['Shanghai', 'Nantong', 'Suzhou', 'Hangzhou', 'Ningbo']
cost_btw_cities = [
('Shanghai', 'Nantong', 1),
('Nantong', 'Suzhou', 1),
('Suzhou', 'Shanghai', 1),
('Suzhou', 'Hangzhou', 3),
('Hangzhou', 'Ningbo', 2),
('Hangzhou', 'Shanghai', 2),
('Ningbo', 'Shanghai', 2)
]
self.assert_power_supply_cost(cities, cost_btw_cities, 6) # (Shanghai, Nantong), (Shanghai, Suzhou), (Shanghai, Hangzhou), (Shanghai, Nantong)
if __name__ == '__main__':
unittest.main(exit=False)
Jul 5, 2019 [Hard] Order of Course Prerequisites
Question: We’re given a hashmap associating each courseId key with a list of courseIds values, which represents that the prerequisites of courseId are courseIds. Return a sorted ordering of courses such that we can finish all courses.
Return null if there is no such ordering.
For example, given
{'CSC300': ['CSC100', 'CSC200'], 'CSC200': ['CSC100'], 'CSC100': []}, should return['CSC100', 'CSC200', 'CSC300'].
My thoughts: This is a pretty standard application of Topological Sort. One thing you need to be careful is that the given prerequisites map is not the neighbor map, we need to first reverse all edge to generate a neighbor map. And another matter you might ignore is that the during interview you might be asked to test your result. In that case, stick with the definition of topological sort. For any edge (u, v), the index of u is always smaller than the index of v in topological order.
Solution with Topological Sort: https://repl.it/@trsong/Order-of-Course-Prerequisites
import unittest
class CourseState:
FINISHED = 0
TAKING = 1
TO_TAKE = 2
def sort_courses(prereq_map):
# Add all course to neighbor
neighbor = { course: [] for course in prereq_map }
# Add all prereq course to neighbor
for course, prereq_list in prereq_map.iteritems():
for prereq in prereq_list:
if prereq not in neighbor:
neighbor[prereq] = []
neighbor[prereq].append(course)
course_states = { course: CourseState.TO_TAKE for course in neighbor }
stack = []
topological_order = []
for course in neighbor:
# For each unvisited course do a DFS search
if course_states[course] != CourseState.FINISHED:
stack.append(course)
while stack:
current_course = stack[-1]
if course_states[current_course] == CourseState.TAKING:
course_states[current_course] = CourseState.FINISHED
elif course_states[current_course] == CourseState.TO_TAKE:
course_states[current_course] = CourseState.TAKING
for next_course in neighbor[current_course]:
if course_states[next_course] == CourseState.TAKING:
return None
elif course_states[next_course] == CourseState.TO_TAKE:
stack.append(next_course)
else:
topological_order.append(stack.pop())
topological_order.reverse()
return topological_order
class SortCourseSpec(unittest.TestCase):
def assert_course_order_with_prereq_map(self, prereq_map):
# Test utility for validation of the following properties for each course:
# 1. no courses can be taken before its prerequisites
# 2. order covers all courses
orders = sort_courses(prereq_map)
self.assertEqual(len(prereq_map), len(orders))
# build a quick courseId to index lookup
course_priority_map = dict(zip(orders, xrange(len(orders))))
for course, prereq_list in prereq_map.iteritems():
for prereq in prereq_list:
# Any prereq course must be taken before the one that depends on it
self.assertTrue(course_priority_map[prereq] < course_priority_map[course])
def test_courses_with_mutual_dependencies(self):
prereq_map = {
'CS115': ['CS135'],
'CS135': ['CS115']
}
self.assertIsNone(sort_courses(prereq_map))
def test_courses_within_same_department(self):
prereq_map = {
'CS240': [],
'CS241': [],
'MATH239': [],
'CS350': ['CS240', 'CS241', 'MATH239'],
'CS341': ['CS240'],
'CS445': ['CS350', 'CS341']
}
self.assert_course_order_with_prereq_map(prereq_map)
def test_courses_in_different_departments(self):
prereq_map = {
'MATH137': [],
'CS116': ['MATH137', 'CS115'],
'JAPAN102': ['JAPAN101'],
'JAPAN101': [],
'MATH138': ['MATH137'],
'ENGL119': [],
'MATH237': ['MATH138'],
'CS246': ['MATH138', 'CS116'],
'CS115': []
}
self.assert_course_order_with_prereq_map(prereq_map)
def test_courses_without_dependencies(self):
prereq_map = {
'ENGL119': [],
'ECON101': [],
'JAPAN101': [],
'PHYS111': []
}
self.assert_course_order_with_prereq_map(prereq_map)
if __name__ == '__main__':
unittest.main(exit=False)
Additional Question: [Special] Find Cycle in Undirected Graph using Disjoint Set (Union-Find)
Question: Given an undirected graph, check if there is a cycle in the graph using Disjoint Set (Union-Find).
Note: A disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. A union-find algorithm is an algorithm that peforms two useful operations on such a data structure:
Find(e): Determine which subset a particular element e is in. This can be used for determining if two elements are in the same subset.
Union(e1, e2): Join two subsets(contains e1 and e2 separately) into a single subset.
Example:
is_cyclic(vertices=3, edges=[(0, 1), (0, 2), (1, 2)]) # returns True, cycle: 0, 1, 2, 0
is_cyclic(vertices=3, edges=[(0, 1), (0, 2)]) # returns False
Solution with Disjoint Set: https://repl.it/@trsong/Find-Cycle-in-Undirected-Graph
import unittest
class DisjointSet(object):
def __init__(self, n):
self._parent = [-1] * n
def find(self, p):
while self._parent[p] != -1:
p = self._parent[p]
return p
def union(self, p1, p2):
parent1 = self.find(p1)
parent2 = self.find(p2)
if parent1 != parent2:
self._parent[parent1] = parent2
def is_connected(self, p1, p2):
return self.find(p1) == self.find(p2)
def is_cyclic(vertices, edges):
uf = DisjointSet(vertices)
for edge in edges:
# For each edge, connect vertices of both ends
u, v = edge
if uf.is_connected(u, v):
# Before we connect both ends, it's already connected, then there must exist a cycle
return True
else:
uf.union(u, v)
return False
class IsCyclicSpec(unittest.TestCase):
def test_graph_with_cycle(self):
self.assertTrue(is_cyclic(3, [(0, 1), (1, 2), (0, 2)]))
def test_disconnected_graph(self):
self.assertFalse(is_cyclic(4, [(0, 1), (2, 3)]))
self.assertFalse(is_cyclic(2, []))
def test_tree(self):
self.assertFalse(is_cyclic(6, [(0, 1), (1, 3), (1, 4), (0, 2), (2, 5)]))
def test_star(self):
self.assertTrue(is_cyclic(5, [(0, 1), (1, 2), (2, 3), (3, 4), (4, 0)]))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 4, 2019 [Easy] Permutations
Question: Given a number in the form of a list of digits, return all possible permutations.
For example, given
[1,2,3], return[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]].
My thoughts: For problem with size k, we swap the n - k th element with the result from problem with size n - 1.
Example:
permutation(n) = swap a[0] with each elem of permutation(n-1).
permutation(k) = swap a[n - k] with each elem of permutation(k-1)
Suppose the input is [0, 1, 2]
├ swap(0, 0)
│ ├ swap(1, 1)
│ │ └ swap(2, 2) gives [0, 1, 2]
│ └ swap(1, 2)
│ └ swap(2, 2) gives [0, 2, 1]
├ swap(0, 1)
│ ├ swap(1, 1)
│ │ └ swap(2, 2) gives [1, 0, 2]
│ └ swap(1, 2)
│ └ swap(2, 2) gives [1, 2, 0]
└ swap(0, 2)
├ swap(1, 1)
│ └ swap(2, 2) gives [2, 1, 0]
└ swap(1, 2)
└ swap(2, 2) gives [2, 0, 1]
Solution with Backtrack: https://repl.it/@trsong/Permutations
import unittest
def calculate_permutations(nums):
res = []
n = len(nums)
def swap_pos_recur(pos):
if pos == n - 1:
res.append(nums[:])
for i in xrange(pos, len(nums)):
nums[i], nums[pos] = nums[pos], nums[i]
swap_pos_recur(pos + 1)
# reset position
nums[i], nums[pos] = nums[pos], nums[i]
swap_pos_recur(0)
return res
class CalculatePermutationSpec(unittest.TestCase):
def test_permuation_of_empty_array(self):
self.assertEqual(calculate_permutations([]), [])
def test_permuation_of_2(self):
self.assertEqual(
sorted(calculate_permutations([0, 1])),
sorted([[0, 1], [1, 0]]))
def test_permuation_of_3(self):
self.assertEqual(
sorted(calculate_permutations([1, 2, 3])),
sorted([[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 3, 2019 [Medium] Off-by-One Non-Decreasing Array
Question: Given an array of integers, write a function to determine whether the array could become non-decreasing by modifying at most 1 element.
For example, given the array [10, 5, 7], you should return true, since we can modify the 10 into a 1 to make the array non-decreasing.
Given the array [10, 5, 1], you should return false, since we can’t modify any one element to get a non-decreasing array.
Solution: https://repl.it/@trsong/Off-Most-by-One-Non-Decreasing-Array
import unittest
def is_off_most_by_one_array(arr):
# array of length at most 2 are always qualified
if not arr or len(arr) <= 2: return True
# set up a base for us to compare to and check every later numbers are smaller
base = arr[0]
num_violated = 0
# if the head is not a qualified one alreay, we choose next one as base
if arr[0] > arr[1] and arr[0] > arr[2]:
base = arr[1]
num_violated = 1
for num in arr[1:]:
# any one after base should not be smaller than base
if num < base:
num_violated += 1
# we can tolerate at most one violation
if num_violated >= 2:
return False
else:
base = num
return True
class IsOffMostByOneArraySpec(unittest.TestCase):
def test_empty_array(self):
self.assertTrue(is_off_most_by_one_array([]))
def test_one_element_array(self):
self.assertTrue(is_off_most_by_one_array([1]))
def test_two_elements_array(self):
self.assertTrue(is_off_most_by_one_array([1, 1]))
self.assertTrue(is_off_most_by_one_array([1, 0]))
self.assertTrue(is_off_most_by_one_array([0, 1]))
def test_decreasing_array(self):
self.assertFalse(is_off_most_by_one_array([8, 2, 0]))
def test_non_decreasing_array(self):
self.assertTrue(is_off_most_by_one_array([0, 0, 1, 2, 2]))
self.assertTrue(is_off_most_by_one_array([0, 1, 2]))
self.assertTrue(is_off_most_by_one_array([0, 0, 0, 0]))
def test_off_by_one_array(self):
self.assertTrue(is_off_most_by_one_array([2, 10, 0]))
self.assertTrue(is_off_most_by_one_array([5, 2, 10]))
self.assertTrue(is_off_most_by_one_array([10, 5, 7]))
def test_off_by_two_array(self):
self.assertFalse(is_off_most_by_one_array([5, 2, 10, 3, 4]))
self.assertFalse(is_off_most_by_one_array([0, 1, 0, 0, 0, 1]))
self.assertFalse(is_off_most_by_one_array([1, 1, 0, 0]))
if __name__ == '__main__':
unittest.main(exit=False)
Additional Question: [Special] Longest Path in A Directed Acyclic Graph
Question: Given a Directed Acyclic Graph (DAG), find the longest distances in the given graph.
Note: The longest path problem for a general graph is not as easy as the shortest path problem because the longest path problem doesn’t have optimal substructure property. In fact, the Longest Path problem is NP-Hard for a general graph. However, the longest path problem has a linear time solution for directed acyclic graphs. The idea is similar to linear time solution for shortest path in a directed acyclic graph. We use Topological Sorting.
Example:
# Following returns 3, as longest path is: 5, 2, 3, 1
longest_path_in_DAG(vertices=6, edges=[(5, 2), (5, 0), (4, 0), (4, 1), (2, 3), (3, 1)])
Solution with DFS Sorting in Topological Order: https://repl.it/@trsong/Longest-Path-in-A-Directed-Acyclic-Graph
import unittest
class VertexState(object):
UNVISITED = 0
VISITING = 1
VISITED = 2
def longest_path_in_DAG(vertices, edges):
stack = []
prev = [-1] * vertices
vertex_states = [VertexState.UNVISITED] * vertices
neibor = [None] * vertices
topological_order = []
for pair in edges:
if not neibor[pair[0]]:
neibor[pair[0]] = []
neibor[pair[0]].append(pair[1])
for v in xrange(vertices):
if vertex_states[v] != VertexState.VISITED:
stack.append(v)
while stack:
current = stack[-1]
if vertex_states[current] == VertexState.VISITING:
vertex_states[current] = VertexState.VISITED
elif vertex_states[current] == VertexState.UNVISITED:
vertex_states[current] = VertexState.VISITING
if neibor[current]:
for n in neibor[current]:
if vertex_states[n] == VertexState.VISITING:
# if trying to access a visiting vertex, then it indicates that edge is a back edge
return -1
if vertex_states[n] == VertexState.UNVISITED:
prev[n] = current
stack.append(n)
else:
# if current state is VISITED
topological_order.append(stack.pop())
distance = [-1] * vertices
for v in xrange(vertices):
if prev[v] == -1:
distance[v] = 0
while topological_order:
current = topological_order.pop()
if distance[current] != -1:
if neibor[current]:
for n in neibor[current]:
distance[n] = max(distance[n], distance[current] + 1)
return max(distance)
class LongestPathInDAGSpec(unittest.TestCase):
def test_grap_with_cycle(self):
v = 3
e = [(0, 1), (2, 0), (1, 2)]
self.assertEqual(longest_path_in_DAG(v, e), -1)
v = 2
e = [(0, 1), (0, 0)]
self.assertEqual(longest_path_in_DAG(v, e), -1)
def test_disconnected_graph(self):
v = 5
e = [(0, 1), (2, 3), (3, 4)]
self.assertEqual(longest_path_in_DAG(v, e), 2) # path: 2, 3, 4
def test_graph_with_two_paths(self):
v = 5
e = [(0, 1), (1, 4), (0, 2), (2, 3), (3, 4)]
self.assertEqual(longest_path_in_DAG(v, e), 3) # path: 0, 2, 3, 4
e = [(0, 2), (2, 3), (3, 4), (0, 1), (1, 4)]
self.assertEqual(longest_path_in_DAG(v, e), 3) # path: 0, 2, 3, 4
def test_connected_graph_with_paths_of_different_lenghths(self):
v = 7
e = [(0, 2), (0, 3), (1, 2), (1, 3), (2, 3), (2, 5), (3, 4), (3, 5), (3, 6), (2, 5), (5, 6)]
self.assertEqual(longest_path_in_DAG(v, e), 4) # path: 0, 2, 3, 5, 6
if __name__ == '__main__':
unittest.main(exit=False)
Jul 2, 2019 [Hard] The Longest Increasing Subsequence
Question: Given an array of numbers, find the length of the longest increasing subsequence in the array. The subsequence does not necessarily have to be contiguous.
For example, given the array
[0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15], the longest increasing subsequence has length 6: it is 0, 2, 6, 9, 11, 15.Definition of Subsequence: A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements. For example, the sequence
[A, B, D]is a subsequence of[A, B, C, D, E, F]obtained after removal of elements C, E, and F.
My thoughts: Try different examples until find a pattern to break problem into smaller subproblems. I tried [1, 2, 3, 0, 2], [1, 2, 3, 0, 6], [4, 5, 6, 7, 1, 2, 3] and notice the pattern that the longest increasing subsequence ends at index i equals 1 + max of all previous longest increasing subsequence ends before i if that elem is smaller than sequence[i].
Example, suppose f represents the longest increasing subsequence ends at last element
f([1, 2, 3, 0, 2]) = 1 + max(f([1]), f([1, 2, 3, 0])) # as 2 > 1 and 2 > 0, gives [1, 2], [0, 2] and max len is 2
f([1, 2, 3, 0, 6]) = 1 + max(f[1], f([1, 2]), f([1, 2, 3]), f([1, 2, 3, 0])) # as 6 > all. gives [1, 6], [1, 2, 6] or [1, 2, 3, 6] and max len is 4
And finally once we get an array of all the longest increasing subsequence ends at i. We can take the maximum to find the global longest increasing subsequence among all i.
Solution with DP: https://repl.it/@trsong/The-Longest-Increasing-Subsequence
import unittest
def longest_increasing_subsequence(sequence):
if not sequence: return 0
# let dp[i] represents longest increasing subsequence ends at i, that is,
# dp[i] = the max number of elem j such that sequence[i] > sequence[j] for all 0 <= j < i
# dp[i] = 1 + max(dp[j]) if sequence[i] > sequence[j]
# or, dp[i] = 1 if j not exists
n = len(sequence)
dp = [1] * n
for i in xrange(n):
max_dp_so_far = 0
for j in xrange(i):
if sequence[i] > sequence[j]:
max_dp_so_far = max(max_dp_so_far, dp[j])
dp[i] += max_dp_so_far
return max(dp)
class LongestIncreasingSubsequnceSpec(unittest.TestCase):
def test_empty_sequence(self):
self.assertEqual(longest_increasing_subsequence([]), 0)
def test_last_elem_is_local_max(self):
self.assertEqual(longest_increasing_subsequence([1, 2, 3, 0, 2]), 3)
def test_last_elem_is_global_max(self):
self.assertEqual(longest_increasing_subsequence([1, 2, 3, 0, 6]), 4)
def test_longest_increasing_subsequence_in_first_half_sequence(self):
self.assertEqual(longest_increasing_subsequence([4, 5, 6, 7, 1, 2, 3]), 4)
def test_longest_increasing_subsequence_in_second_half_sequence(self):
self.assertEqual(longest_increasing_subsequence([1, 2, 3, -2, -1, 0, 1]), 4)
def test_sequence_in_up_down_up_pattern(self):
self.assertEqual(longest_increasing_subsequence([1, 2, 3, 2, 4]), 4)
self.assertEqual(longest_increasing_subsequence([1, 2, 3, -1, 0]), 3)
def test_sequence_in_down_up_down_pattern(self):
self.assertEqual(longest_increasing_subsequence([4, 3, 5]), 2)
self.assertEqual(longest_increasing_subsequence([4, 0, 1]), 2)
if __name__ == '__main__':
unittest.main(exit=False)
Additional Question: [Special] Strongly Connected Directed Graph
Question: Given a directed graph, find out whether the graph is strongly connected or not. A directed graph is strongly connected if there is a path between any two pair of vertices.
Example:
is_SCDG(vertices=5, edges=[(0, 1), (1, 2), (2, 3), (3, 0), (2, 4), (4, 2)]) # returns True
is_SCDG(vertices=4, edges=[(0, 1), (1, 2), (2, 3)]) # returns False
My thoughts: A directed graph being strongly connected indicates that for any vertex v, there exists a path to all other vertices and for all other vertices there exists a path to v. Here we can just pick any vertex from which we run DFS and see if it covers all vertices. And once done that, we can show v can go to all other vertices (excellent departure). Then we reverse the edges and run DFS from v again to test if v can be reach by all other vertices (excellent destination).
Therefore, as v can be connected from any other vertices as well as can be reach by any other vertices. For any vertices u, w, we can simply connect them to v to reach each other. Thus, we can show such algorithm can test if a directed graph is strongly connected or not.
Solution with DFS: https://repl.it/@trsong/Strongly-Connected-Directed-Graph
import unittest
def can_reach_all_DFS(s, neighbors, num_vertices):
stack = [s]
visited = [False] * num_vertices
count = 0
while stack:
cur = stack.pop()
if not visited[cur]:
count += 1
visited[cur] = True
if cur in neighbors:
stack.extend(neighbors[cur])
return count == num_vertices
def is_SCDG(vertices, edges):
forward_neighbors = {}
for pair in edges:
if pair[0] not in forward_neighbors:
forward_neighbors[pair[0]] = []
forward_neighbors[pair[0]].append(pair[1])
if not can_reach_all_DFS(0, forward_neighbors, vertices): return False
backward_neighbors = {}
for pair in edges:
if pair[1] not in backward_neighbors:
backward_neighbors[pair[1]] = []
backward_neighbors[pair[1]].append(pair[0])
return can_reach_all_DFS(0, backward_neighbors, vertices)
class IsSCDGSpec(unittest.TestCase):
def test_unconnected_graph(self):
self.assertFalse(is_SCDG(3, [(0, 1), (1, 0)]))
def test_strongly_connected_graph(self):
self.assertTrue(is_SCDG(5, [(0, 1), (1, 2), (2, 3), (3, 0), (2, 4), (4, 2)]))
def test_not_strongly_connected_graph(self):
self.assertFalse(is_SCDG(4, [(0, 1), (1, 2), (2, 3)]))
if __name__ == '__main__':
unittest.main(exit=False)
Jul 1, 2019 [Medium] Merge K Sorted Lists
Question: Given k sorted singly linked lists, write a function to merge all the lists into one sorted singly linked list.
My thoughts: When merging two sorted lists, we always append to result the smaller element between those two lists until both of the lists are exhausted. The same idea applys to merging k sorted list. For each iteration, we always append to result the smallest elements (i.e global smallest) among all k lists. Each list from the k sorted list will have a pointer refer to the next available element to be processed. And in order to quickly identify the global smallest, we can use a priority queue to keep track of the pointer to the smallest element.
Solution with Priority Queue: https://repl.it/@trsong/Merge-K-Sorted-Lists
import unittest
from queue import PriorityQueue
class ListNode(object):
def __init__(self, x, next=None):
self.val = x
self.next = next
def __eq__(self, other):
return other is not None and self.val == other.val and self.next == other.next
def List(*vals):
dummy = ListNode(-1)
p = dummy
for elem in vals:
p.next = ListNode(elem)
p = p.next
return dummy.next
def merge_k_sorted_lists(lists):
if not lists: return List()
# priority queue contains smallest among all sub_list
pq = PriorityQueue()
# Iterate through the list and put local min value from each sub-list into priority queue
lst_ptr = lists
while lst_ptr:
sub_list_ptr = lst_ptr.val
if sub_list_ptr:
pq.put((sub_list_ptr.val, sub_list_ptr))
lst_ptr = lst_ptr.next
res_dummy = ListNode(-1)
p = res_dummy
while not pq.empty():
# Pop the head of priority queue as it contains global min value
min_val, min_ptr = pq.get()
p.next = ListNode(min_val)
p = p.next
min_ptr = min_ptr.next
if min_ptr:
pq.put((min_ptr.val, min_ptr))
return res_dummy.next
class MergeKSortedListSpec(unittest.TestCase):
def test_empty_list(self):
self.assertEqual(merge_k_sorted_lists(List()), List())
def test_list_contains_empty_sub_lists(self):
lists = List(List(), List(), List(1), List(), List(2), List(0, 4))
self.assertEqual(merge_k_sorted_lists(lists), List(0, 1, 2, 4))
def test_sub_lists_with_duplicated_values(self):
lists = List(List(1, 1, 3), List(1), List(3), List(1, 2), List(2, 3), List(2, 2), List(3))
self.assertEqual(merge_k_sorted_lists(lists), List(1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3))
def test_general_lists(self):
lists = List(
List(),
List(1, 4, 7, 15),
List(),
List(2),
List(0, 3, 9, 10),
List(8, 13),
List(),
List(11, 12, 14),
List(5, 6)
)
self.assertEqual(merge_k_sorted_lists(lists), List(*range(16)))
if __name__ == '__main__':
unittest.main(exit=False)
June 30, 2019 [Special] Implementing Priority Queue with Heap
Question: The heap data structure with the
heapify_downandheapify_upoperations can efficiently implement a priority queue that is constrained to hold at most N elements at any point in time. Implementing the following methods for priority queue with heap:
insert(v)inserts the item v into heap.find_min()identifies the minimum element but does not remove it.delete(i)deletes the element in heap position i.extract_min()identifies and deletes an element with minimum key value from a heap.
My thoughts: When insert an element to priority queue, append it to tail of heap and bubble-up that element. When remove an element, swap that element with last element and bubble-down that element.
Implementing Priority Queue with Heap: https://repl.it/@trsong/Implementing-Priority-Queue-with-Heap
import unittest
class Heap(object):
@staticmethod
def heapify(arr):
# Heapify starts from last internal node. i.e. Last elem of (n - 1)'s parent
for i in xrange(len(arr) / 2 - 1, -1, -1):
Heap.heapify_down(arr, i)
@staticmethod
def heapify_down(arr, index=0):
# Bubble-down arr[index] until not possible
n = len(arr)
while True:
left_child = 2 * index + 1
right_child = left_child + 1
smaller_child = left_child
if right_child < n and arr[right_child] < arr[left_child]:
smaller_child = right_child
if smaller_child < n and arr[index] > arr[smaller_child]:
arr[index], arr[smaller_child] = arr[smaller_child], arr[index]
index = smaller_child
else:
break
@staticmethod
def heapify_up(arr, index=None):
# Bubble-up arr[index] until not possible
if index is None:
index = len(arr) - 1
while index > 0:
parent = (index + 1) / 2 - 1
if arr[parent] <= arr[index]:
break
else:
arr[parent], arr[index] = arr[index], arr[parent]
index = parent
class HeapSpec(unittest.TestCase):
def test_heapify_up(self):
"""
0
/ \
2 5
/ \ /
6 3 1
"""
arr = [0, 2, 5, 6, 3, 1]
Heap.heapify_up(arr)
"""
0
/ \
2 1
/ \ /
6 3 5
"""
self.assertEqual(arr, [0, 2, 1, 6, 3, 5])
def test_heapify_down(self):
"""
4
/ \
2 5
/ \ /
6 3 1
"""
arr = [4, 2, 5, 6, 3, 1]
Heap.heapify_down(arr)
"""
2
/ \
3 5
/ \ /
6 4 1
"""
self.assertEqual(arr, [2, 3, 5, 6, 4, 1])
class PriorityQueue(object):
def __init__(self, arr=None):
self._heap = arr[:] if arr else []
Heap.heapify(self._heap)
def insert(self, v):
self._heap.append(v)
Heap.heapify_up(self._heap)
def find_min(self):
return self._heap[0]
def delete(self, i):
last = self._heap.pop()
if self._heap:
self._heap[i] = last
parent = (i + 1) / 2 - 1
if parent >= 0 and self._heap[i] < self._heap[parent]:
Heap.heapify_up(self._heap, index=i)
else:
Heap.heapify_down(self._heap, index=i)
def extract_min(self):
min_val = self.find_min()
self.delete(0)
return min_val
class PriorityQueueSpec(unittest.TestCase):
def assert_priority_queue(self, numbers, expected):
pq = PriorityQueue()
for e in numbers:
pq.insert(e)
for r in expected:
self.assertEqual(pq.find_min(), r)
self.assertEqual(pq.extract_min(), r)
def test_decreasing_inputs(self):
self.assert_priority_queue([5, 4, 3, 2, 1], [1, 2, 3, 4, 5])
def test_random_inputs(self):
self.assert_priority_queue([1, 5, 2, 4, 3], [1, 2, 3, 4, 5])
def test_delete(self):
pq = PriorityQueue()
for i in xrange(6, -1, -1):
pq.insert(i)
pq.delete(4)
self.assertEqual(pq.extract_min(), 0)
pq.insert(7)
self.assertEqual(pq.extract_min(), 1)
self.assertEqual(pq.extract_min(), 2)
def test_construct_heap(self):
pq = PriorityQueue([6, 5, 4, 3, 2, 1, 0])
for i in xrange(7):
self.assertEqual(pq.extract_min(), i)
pq = PriorityQueue([0, 1, 2, 3, 4, 5, 6])
for i in xrange(7):
self.assertEqual(pq.extract_min(), i)
pq = PriorityQueue([6, 1, 5, 2, 0, 4, 3])
for i in xrange(7):
self.assertEqual(pq.extract_min(), i)
if __name__ == '__main__':
unittest.main(exit=False)
June 29, 2019 [Hard] Largest Sub BST Size
Question: Given a binary tree, find the size of the largest tree/subtree that is a Binary Search Tree (BST).
Examples:
Input:
5
/ \
2 4
/ \
1 3
Output: 3
The following subtree is the maximum size BST subtree
2
/ \
1 3
Input:
50
/ \
30 60
/ \ / \
5 20 45 70
/ \
65 80
Output: 5
The following subtree is the maximum size BST subtree
60
/ \
45 70
/ \
65 80
My thoughts: This problem is similar to finding height of binary tree where post-order traversal is used. The idea is to gather infomation from left and right tree to determine if current node forms a valid BST or not through checking if the value fit into the range. And the infomation from children should contain if children are valid BST, the min & max of subtree and accumulated largest sub BST size.
Solution with Post-Order Tree Traversal: https://repl.it/@trsong/Largest-Sub-BST-Size
import unittest
class Node(object):
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def largest_sub_BST_size_helper(tree):
# Consume a tree node, return boolean, range, number where
# - boolean is True if tree is valid BST,
# - range is a tuple represent min and max of tree,
# - number is underneath largest sub BST size
if not tree:
return True, None, 0
else:
is_left_BST, left_range, left_size = largest_sub_BST_size_helper(tree.left)
is_right_BST, right_range, right_size = largest_sub_BST_size_helper(tree.right)
# check if left subtree max <= current value <= right subtree min
is_current_BST = (not left_range or left_range[1] <= tree.val) and (not right_range or right_range[0] >= tree.val)
if is_left_BST and is_right_BST and is_current_BST:
left_min = left_range[0] if left_range else tree.val
right_max = right_range[1] if right_range else tree.val
return True, (left_min, right_max), 1 + left_size + right_size
else:
return False, None, max(left_size, right_size)
def largest_sub_BST_size(tree):
return largest_sub_BST_size_helper(tree)[-1]
class LargestSubBSTSizeSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertEqual(largest_sub_BST_size(None), 0)
def test_right_heavy_tree(self):
"""
1
\
10
/ \
11 28
"""
n11, n28 = Node(11), Node(28)
n10 = Node(10, n11, n28)
n1 = Node(1, right=n10)
self.assertEqual(largest_sub_BST_size(n1), 1)
def test_left_heavy_tree(self):
"""
0
/
3
/
2
/
1
"""
n1 = Node(1)
n2 = Node(2, n1)
n3 = Node(3, n2)
n0 = Node(0, n3)
self.assertEqual(largest_sub_BST_size(n0), 3)
def test_largest_BST_on_left_subtree(self):
"""
0
/ \
2 -2
/ \ \
1 3 -1
"""
n2 = Node(2, Node(1), Node(3))
n2m = Node(2, right=Node(-1))
n0 = Node(0, n2, n2m)
self.assertEqual(largest_sub_BST_size(n0), 3)
def test_largest_BST_on_right_subtree(self):
"""
50
/ \
30 60
/ \ / \
5 20 45 70
/ \
65 80
"""
n30 = Node(30, Node(5), Node(20))
n70 = Node(70, Node(65), Node(80))
n60 = Node(60, Node(45), n70)
n50 = Node(50, n30, n60)
self.assertEqual(largest_sub_BST_size(n50), 5)
if __name__ == '__main__':
unittest.main(exit=False)
June 28, 2019 [Special] Stable Marriage Problem
Question: The Stable Marriage Problem states that given N men and N women, where each person has ranked all members of the opposite sex in order of preference, marry the men and women together such that there are no two people of opposite sex who would both rather have each other than their current partners. If there are no such people, all the marriages are “stable” (Wiki Source: https://en.wikipedia.org/wiki/Stable_marriage_problem).
Consider the following example.
Let there be two men m1 and m2 and two women w1 and w2.
Let m1's list of preferences be {w1, w2}
Let m2's list of preferences be {w1, w2}
Let w1's list of preferences be {m1, m2}
Let w2's list of preferences be {m1, m2}
The matching { {m1, w2}, {w1, m2} } is not stable because m1 and w1 would prefer each other over their assigned partners. The matching {m1, w1} and {m2, w2} is stable because there are no two people of opposite sex that would prefer each other over their assigned partners.
Input: Input is a 2D matrix of size (2 * N) * N where N is number of women or men. Rows from 0 to N-1 represent preference lists of women and rows from N to 2 * N – 1 represent preference lists of men. So women are numbered from 0 to N-1 and men are numbered from N to 2 * N – 1.
Output: A list of married pairs (woman, man).
Example, suppose Men = {0, 1, 2, 3} and Women = {4, 5, 6, 7}:
[
# Woman Preference Lists
[7, 5, 6, 4],
[5, 4, 6, 7],
[4, 5, 6, 7],
[4, 5, 6, 7],
# Man Preference Lists
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
]
Should produce:
[(4,2), (5,1), (6,3), (7, 0)]
Note: Solution might not be unique.
Pseudocode for Gale–Shapley Algorithm:
function stableMatching {
Initialize all m ∈ M and w ∈ W to free
while ∃ free man m who still has a woman w to propose to {
w = first woman on m’s list to whom m has not yet proposed
if w is free
(m, w) become engaged
else some pair (m', w) already exists
if w prefers m to m'
m' becomes free
(m, w) become engaged
else
(m', w) remain engaged
}
}
Solution with Gale–Shapley Algorithm: https://repl.it/@trsong/Stable-Marriage-Problem
import unittest
from collections import deque
class StableMarriageProblem(object):
@staticmethod
def solve(preference_lists):
num_couple = len(preference_lists) / 2
woman_engagement = [None] * num_couple
woman_preference_ranking = [[0 for _ in xrange(2 * num_couple)] for _ in xrange(num_couple)]
unproposed_men = deque(range(num_couple, len(preference_lists)))
man_next_propose_index = [0] * num_couple
# Pre-process woman preference_lists to generate ranking list for quick look-up
for woman in xrange(num_couple):
for rank, candidate in enumerate(preference_lists[woman]):
woman_preference_ranking[woman][candidate] = rank
while unproposed_men:
man = unproposed_men.pop()
target_woman_index = man_next_propose_index[man - num_couple]
target_woman = preference_lists[man][target_woman_index]
if not woman_engagement[target_woman]:
woman_engagement[target_woman] = man
elif woman_preference_ranking[target_woman][man] < woman_preference_ranking[target_woman][woman_engagement[target_woman]]:
# if current man is better candidate
evicted_man = woman_engagement[target_woman]
unproposed_men.append(evicted_man)
woman_engagement[target_woman] = man
else:
unproposed_men.appendleft(man)
man_next_propose_index[man - num_couple] += 1
married_couples = []
for woman, man in enumerate(woman_engagement):
married_couples.append((woman, man))
return married_couples
@staticmethod
def calc_instability_pairs(preference_lists, married_pairs):
# Calculate all instability pairs based on Preference_lists and Married_pairs
chosen = dict(married_pairs)
chosen.update((p[1], p[0]) for p in married_pairs)
def rank(person, target):
return preference_lists[person].index(target)
def has_better_choice(person, target):
return rank(person, target) < rank(person, chosen[person])
instability_pairs = []
for person, preference_list in enumerate(preference_lists):
for candidate in preference_list:
if chosen[person] != candidate and has_better_choice(person, candidate) and has_better_choice(candidate, person):
# check if exists (person, candidate) not in married_pairs such that
# rank(person, candidate) < rank(person, chosen[person]) and
# rank(candidate, person) < rank(candidate, chosen[candidate])
instability_pairs.append((person, candidate))
return instability_pairs
class StableMarriageProblemSpec(unittest.TestCase):
def test_unstable_marriage_should_return_correct_instability_pairs(self):
# Test utility method calc_instability_pairs
preference_lists = [
# Woman Preference Lists
[2, 3],
[2, 3],
# Man Preference Lists
[0, 1],
[0, 1]
]
married_pairs = [(0, 3), (1, 2)]
instability_pairs = [(0, 2), (2, 0)]
self.assertEqual(StableMarriageProblem.calc_instability_pairs(preference_lists, married_pairs), instability_pairs)
def assert_perfect_stable_marriage(self, preference_lists):
# Check if all people are married as well as all married_pairs are stable
married_pairs = StableMarriageProblem.solve(preference_lists)
num_couple = len(preference_lists) / 2
self.assertEqual(len(married_pairs), num_couple)
self.assertFalse(StableMarriageProblem.calc_instability_pairs(preference_lists, married_pairs))
def test_sample_preference_lists(self):
self.assert_perfect_stable_marriage([
# Woman Preference Lists
[7, 5, 6, 4],
[5, 4, 6, 7],
[4, 5, 6, 7],
[4, 5, 6, 7],
# Man Preference Lists
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
])
if __name__ == '__main__':
unittest.main(exit=False)
June 27, 2019 [Medium] Isolated Islands
Question: Given a matrix of 1s and 0s, return the number of “islands” in the matrix. A 1 represents land and 0 represents water, so an island is a group of 1s that are neighboring whose perimeter is surrounded by water.
For example, this matrix has 4 islands.
1 0 0 0 0
0 0 1 1 0
0 1 1 0 0
0 0 0 0 0
1 1 0 0 1
1 1 0 0 1
My thoughts: This is a pretty standard DFS/BFS question. The idea is to scan through and count all unvisited cells with value 1 and mark all neighbors “connected” (also have value 1) as visited.
DFS Solution: https://repl.it/@trsong/Isolated-Islands
import unittest
def is_valid_pos(row, col, area_map):
n, m = len(area_map), len(area_map[0])
return 0 <= row < n and 0 <= col < m
def get_neighbors(pos, area_map, visited):
r, c = pos
for row in [r-1, r, r+1]:
for col in [c-1, c, c+1]:
if is_valid_pos(row, col, area_map):
yield row, col
def DFS_mark_neighbor_cells(pos, area_map, visited):
stack = [pos]
while stack:
r, c = stack.pop()
if area_map[r][c] and not visited[r][c]:
visited[r][c] = True
stack.extend(get_neighbors((r, c), area_map, visited))
def calc_islands(area_map):
n, m = len(area_map), len(area_map[0])
visited = [[False for _ in xrange(m)] for _ in xrange(n)]
res = 0
for r in xrange(n):
for c in xrange(m):
if area_map[r][c] and not visited[r][c]:
res += 1
DFS_mark_neighbor_cells((r, c), area_map, visited)
return res
class CalcIslandSpec(unittest.TestCase):
def test_sample_area_map(self):
self.assertEqual(calc_islands([
[1, 0, 0, 0, 0],
[0, 0, 1, 1, 0],
[0, 1, 1, 0, 0],
[0, 0, 0, 0, 0],
[1, 1, 0, 0, 1],
[1, 1, 0, 0, 1]
]), 4)
def test_some_random_area_map(self):
self.assertEqual(calc_islands([
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[1, 0, 0, 1, 1],
[0, 0, 0, 0, 0],
[1, 0, 1, 0, 1]
]), 5)
def test_island_edge_of_map(self):
self.assertEqual(calc_islands([
[1, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 0, 0],
[1, 0, 1, 0, 1],
[1, 0, 1, 0, 1]
]), 5)
def test_huge_water(self):
self.assertEqual(calc_islands([
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]
]), 0)
def test_huge_island(self):
self.assertEqual(calc_islands([
[1, 0, 1, 0, 1],
[1, 0, 0, 1, 0],
[1, 1, 1, 0, 1]
]), 1)
if __name__ == '__main__':
unittest.main(exit=False)
June 26, 2019 [Medium] Count Attacking Bishop Pairs
Question: On our special chessboard, two bishops attack each other if they share the same diagonal. This includes bishops that have another bishop located between them, i.e. bishops can attack through pieces.
You are given N bishops, represented as (row, column) tuples on a M by M chessboard. Write a function to count the number of pairs of bishops that attack each other. The ordering of the pair doesn’t matter: (1, 2) is considered the same as (2, 1).
For example, given M = 5 and the list of bishops:
(0, 0)
(1, 2)
(2, 2)
(4, 0)
The board would look like this:
[b 0 0 0 0]
[0 0 b 0 0]
[0 0 b 0 0]
[0 0 0 0 0]
[b 0 0 0 0]
You should return 2, since bishops 1 and 3 attack each other, as well as bishops 3 and 4.
My thoughts: Cell on same diagonal has the following properties:
- Major diagonal: col - row = constant
- Minor diagonal: col + row = constant
Example:
>>> [[r-c for c in xrange(5)] for r in xrange(5)]
[
[0, -1, -2, -3, -4],
[1, 0, -1, -2, -3],
[2, 1, 0, -1, -2],
[3, 2, 1, 0, -1],
[4, 3, 2, 1, 0]
]
>>> [[r+c for c in xrange(5)] for r in xrange(5)]
[
[0, 1, 2, 3, 4],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 6],
[3, 4, 5, 6, 7],
[4, 5, 6, 7, 8]
]
Thus, we can store the number of bishop on the same diagonal and use the formula to calculate n-choose-2: n(n-1)/2
Python Solution: https://repl.it/@trsong/Count-Attacking-Bishop-Pairs
import unittest
def count_attacking_pairs(bishop_positions):
major_diagonal_lookup = {}
minor_diagonal_lookup = {}
for pos in bishop_positions:
major_diagonal = pos[1] - pos[0]
minor_diagonal = pos[1] + pos[0]
if major_diagonal in major_diagonal_lookup:
major_diagonal_lookup[major_diagonal] += 1
else:
major_diagonal_lookup[major_diagonal] = 1
if minor_diagonal in minor_diagonal_lookup:
minor_diagonal_lookup[minor_diagonal] += 1
else:
minor_diagonal_lookup[minor_diagonal] = 1
count = 0
for val in major_diagonal_lookup.values():
count += val * (val - 1) /2
for val in minor_diagonal_lookup.values():
count += val * (val - 1) / 2
return count
class CountAttackingPairSpec(unittest.TestCase):
def test_zero_bishops(self):
self.assertEqual(count_attacking_pairs([]), 0)
def test_zero_attacking_pairs(self):
"""
0 b 0 0
0 b 0 0
0 b 0 0
0 b 0 0
"""
self.assertEqual(count_attacking_pairs([(0, 1), (1, 1), (2, 1), (3, 1)]), 0)
"""
0 0 0 b
b 0 0 0
b 0 b 0
0 0 0 0
"""
self.assertEqual(count_attacking_pairs([(0, 3), (1, 0), (2, 0), (2, 2)]), 0)
def test_no_bishop_between_attacking_pairs(self):
"""
b 0 b
b 0 b
b 0 b
"""
self.assertEqual(count_attacking_pairs([(0, 0), (1, 0), (2, 0), (0, 2), (1, 2), (2, 2)]), 2)
"""
b 0 0 0 0
0 0 b 0 0
0 0 b 0 0
0 0 0 0 0
b 0 0 0 0
"""
self.assertEqual(count_attacking_pairs([(0, 0), (1, 2), (2, 2), (4, 0)]), 2)
def test_has_bishop_between_attacking_pairs(self):
"""
b 0 b
0 b 0
b 0 b
"""
self.assertEqual(count_attacking_pairs([(0, 0), (0, 2), (1, 1), (2, 0), (2, 2)]), 6)
if __name__ == '__main__':
unittest.main(exit=False)
June 25, 2019 LC 239 [Medium] Sliding Window Maximum
Question: Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.
Example:
Input: nums = [1,3,-1,-3,5,3,6,7], and k = 3
Output: [3,3,5,5,6,7]
Explanation:
Window position Max
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
Note: You may assume k is always valid, 1 ≤ k ≤ input array’s size for non-empty array.
Follow up: Could you solve it in linear time?
My thoughts: The idea is to efficiently keep track of INDEX of 1st max, 2nd max, 3rd max and potentially k-th max elem. The reason for storing index is for the sake of avoiding index out of window. We can achieve that by using Double-Ended Queue which allow us to efficiently push and pop from both ends of the queue.
The queue looks like [index of 1st max, index of 2nd max, ...., index of k-th max]
We might run into the following case as we progress:
- index of 1st max is out of bound of window: we pop left and index of 2nd max because 1st max within window
- the next elem become j-th max: evict old j-th max all the way to index of k-th max on the right of dequeue, i.e. pop right:
[index of 1st max, index of 2nd max, ..., index of j-1-th max, index of new elem]
Solution with Double-Ended Queue: https://repl.it/@trsong/Sliding-Window-Maximum
from collections import deque as Deque
import unittest
def max_sliding_window(nums, k):
if not nums: return []
deque = Deque()
res = []
for i, elem in enumerate(nums):
if deque and deque[0] <= i - k:
# index out of range k
deque.popleft()
while deque and nums[deque[-1]] < elem:
# remove index of existing elem in the deque that are smaller than the new elem
deque.pop()
deque.append(i)
if i >= k-1:
# start printing result when deque is populated
res.append(nums[deque[0]])
return res
class MaxSlidingWindowSpec(unittest.TestCase):
def test_empty_array(self):
self.assertEqual(max_sliding_window([], 1), [])
def test_window_has_same_size_as_array(self):
self.assertEqual(max_sliding_window([3, 2, 1], 3), [3])
self.assertEqual(max_sliding_window([1, 2], 2), [2])
self.assertEqual(max_sliding_window([-1], 1), [-1])
def test_non_ascending_array(self):
self.assertEqual(max_sliding_window([4, 3, 3, 2, 2, 1], 2), [4, 3, 3, 2, 2])
self.assertEqual(max_sliding_window([1, 1, 1], 2), [1, 1])
def test_non_descending_array(self):
self.assertEqual(max_sliding_window([1, 1, 2, 2, 2, 3], 3), [2, 2, 2, 3])
self.assertEqual(max_sliding_window([1, 1, 2, 3], 1), [1, 1, 2 ,3])
def test_first_decreasing_then_increasing_array(self):
self.assertEqual(max_sliding_window([5, 4, 1, 1, 1, 2, 2, 2], 3), [5, 4, 1, 2, 2, 2])
self.assertEqual(max_sliding_window([3, 2, 1, 2, 3], 2), [3, 2, 2, 3])
self.assertEqual(max_sliding_window([3, 2, 1, 2, 3], 3), [3, 2, 3])
def test_first_increasing_then_decreasing_array(self):
self.assertEqual(max_sliding_window([1, 2, 3, 2, 1], 2), [2, 3, 3, 2])
self.assertEqual(max_sliding_window([1, 2, 3, 2, 1], 3), [3, 3, 3])
def test_oscillation_array(self):
self.assertEqual(max_sliding_window([1, -1, 1, -1, -1, 1, 1], 2), [1, 1, 1, -1, 1, 1])
self.assertEqual(max_sliding_window([1, 3, 1, 2, 0, 5], 3), [3, 3, 2, 5])
def test_example_array(self):
self.assertEqual(max_sliding_window([1, 3, -1, -3, 5, 3, 6, 7], 3), [3, 3, 5, 5, 6, 7])
if __name__ == '__main__':
unittest.main(exit=False)
June 24, 2019 [Medium] E-commerce Website
Question: You run an e-commerce website and want to record the last N order ids in a log. Implement a data structure to accomplish this, with the following API:
record(order_id): adds the order_id to the logget_last(i): gets the ith last element from the log. i is guaranteed to be smaller than or equal to N.You should be as efficient with time and space as possible.
Solution with Circular Buffer: https://repl.it/@trsong/E-commerce-Website
import unittest
class ECommerceWebsiteOrderService(object):
def __init__(self, capacity):
self._capacity = capacity
self._end_index = 0
self._circular_buffer = [None] * capacity
def record(self, order_id):
self._circular_buffer[self._end_index] = order_id
self._end_index = (self._end_index + 1) % self._capacity
def get_last(self, i):
if 1 <= i <= self._capacity:
index = (self._end_index - i) % self._capacity
return self._circular_buffer[index]
else:
return None
class ECommerceWebsiteSpec(unittest.TestCase):
def test_order_within_capacity(self):
service = ECommerceWebsiteOrderService(4)
self.assertIsNone(service.get_last(1))
service.record(1)
service.record(2)
service.record(3)
self.assertIsNone(service.get_last(-1))
self.assertIsNone(service.get_last(0))
self.assertEqual(service.get_last(1), 3)
self.assertEqual(service.get_last(2), 2)
self.assertEqual(service.get_last(3), 1)
self.assertIsNone(service.get_last(4))
def test_order_overflow_capacity(self):
service = ECommerceWebsiteOrderService(2)
service.record(1)
service.record(2)
self.assertEqual(service.get_last(1), 2)
self.assertEqual(service.get_last(2), 1)
service.record(3)
self.assertEqual(service.get_last(1), 3)
self.assertEqual(service.get_last(2), 2)
service.record(4)
service.record(5)
self.assertEqual(service.get_last(1), 5)
self.assertEqual(service.get_last(2), 4)
self.assertEqual(service.get_last(2), 4)
self.assertIsNone(service.get_last(3))
def test_buffer_has_capacity_one(self):
service = ECommerceWebsiteOrderService(1)
self.assertIsNone(service.get_last(1))
service.record(1)
service.record(2)
self.assertEqual(service.get_last(1), 2)
service.record(3)
self.assertEqual(service.get_last(1), 3)
if __name__ == '__main__':
unittest.main(exit=False)
June 23, 2019 [Easy] Merge Overlapping Intervals
Question: Given a list of possibly overlapping intervals, return a new list of intervals where all overlapping intervals have been merged.
The input list is not necessarily ordered in any way.
For example, given
[(1, 3), (5, 8), (4, 10), (20, 25)], you should return[(1, 3), (4, 10), (20, 25)].
My thoughts: Sort intervals based on start time, then for each consecutive intervals s1, s2 the following could occur:
s1.end < s2.start, we append s2 to results2.start <= s1.end < s2.end, we merge s1 and s2s2.end <= s1.end, s1 overlaps all of s2, we do nothing
Note: as all intervals are sorted based on start time, s1.start <= s2.start
Python Solution: https://repl.it/@trsong/Merge-Overlapping-Intervals
import unittest
def merge_intervals(interval_seq):
if not interval_seq: return []
# sort intervals based on start time
interval_seq.sort(key=lambda interval: interval[0])
stack = [interval_seq[0]]
for interval in interval_seq:
top = stack[-1]
if interval[0] <= top[1] < interval[1]:
stack.pop()
stack.append((top[0], interval[1]))
elif interval[0] > top[1]:
stack.append(interval)
return stack
class MergeIntervalSpec(unittest.TestCase):
def assert_intervals(self, input, expected):
input.sort()
expected.sort()
self.assertEqual(input, expected)
def test_interval_with_zero_mergings(self):
self.assert_intervals(merge_intervals([]), [])
self.assert_intervals(merge_intervals([(1, 2), (3, 4), (5, 6)]), [(1, 2), (3, 4), (5, 6)])
self.assert_intervals(merge_intervals([(-3, -2), (5, 6), (1, 4)]), [(-3, -2), (1, 4), (5, 6)])
def test_interval_with_one_merging(self):
self.assert_intervals(merge_intervals([(1, 3), (5, 7), (7, 11), (2, 4)]), [(1, 4), (5, 11)])
self.assert_intervals(merge_intervals([(1, 4), (0, 8)]), [(0, 8)])
def test_interval_with_two_mergings(self):
self.assert_intervals(merge_intervals([(1, 3), (3, 5), (5, 8)]), [(1, 8)])
self.assert_intervals(merge_intervals([(5, 8), (1, 6), (0, 2)]), [(0, 8)])
def test_interval_with_multiple_mergings(self):
self.assert_intervals(merge_intervals([(-5, 0), (1, 4), (1, 4), (1, 4), (5, 7), (6, 10), (0, 1)]), [(-5, 4), (5, 10)])
self.assert_intervals(merge_intervals([(1, 3), (5, 8), (4, 10), (20, 25)]), [(1, 3), (4, 10), (20, 25)])
if __name__ == '__main__':
unittest.main(exit=False)
June 22, 2019 [Hard] The N Queens Puzzle
Question: You have an N by N board. Write a function that, given N, returns the number of possible arrangements of the board where N queens can be placed on the board without threatening each other, i.e. no two queens share the same row, column, or diagonal.
Hint: Backtracking
My thoughts: Solve the N Queen Problem with Backtracking: place each queen on different columns one by one and test different rows. Mark previous chosen rows and diagonals.
Solution with Backtracking: https://repl.it/@trsong/The-N-Queens-Puzzle
import unittest
def solve_n_queen(n):
"""Solve N Queen Problem with backtracking: place i-th queen on i-th column, count upon success, backtrack when fail """
class Context:
res = 0
def helper(col, prev_rows, prev_row_plus_col, prev_row_minus_col):
if col >= n:
Context.res += 1
return
for row in range(n):
# row_plus_col and row_minus_col are used to mark chosen diagnoal
row_plus_col = row + col
row_minus_col = row - col
if row not in prev_rows and row_plus_col not in prev_row_plus_col and row_minus_col not in prev_row_minus_col:
prev_rows.add(row)
prev_row_plus_col.add(row_plus_col)
prev_row_minus_col.add(row_minus_col)
helper(col + 1, prev_rows, prev_row_plus_col, prev_row_minus_col)
prev_rows.remove(row)
prev_row_plus_col.remove(row_plus_col)
prev_row_minus_col.remove(row_minus_col)
helper(0, set(), set(), set())
return Context.res
class SolveNQueenSpec(unittest.TestCase):
def test_one_queen(self):
self.assertEqual(solve_n_queen(1), 1)
def test_two_three_queen(self):
self.assertEqual(solve_n_queen(2), 0)
self.assertEqual(solve_n_queen(3), 0)
def test_four_queen(self):
self.assertEqual(solve_n_queen(4), 2)
def test_eight_queen(self):
self.assertEqual(solve_n_queen(8), 92)
if __name__ == "__main__":
unittest.main(exit=False)
June 21, 2019 [Medium] Invalid Parentheses to Remove
Question: Given a string of parentheses, write a function to compute the minimum number of parentheses to be removed to make the string valid (i.e. each open parenthesis is eventually closed).
For example, given the string “()())()”, you should return 1. Given the string “)(“, you should return 2, since we must remove all of them.
My thoughts: At any index i, the number of accumulated open-parentheses, ‘(‘, on the left should be greater than or equal to the number of accumulated close-parentheses. And eventually, the total number of open-parentheses should equal the total number of close-parentheses. We simply count all positions violate those two properties.
Python Solution: https://repl.it/@trsong/Invalid-Parentheses-to-Remove
import unittest
def count_invalid_parentheses(input_str):
balance = 0
overflow = 0
for char in input_str:
if char == '(':
balance += 1
elif balance > 0:
balance -= 1
else:
overflow += 1
return balance + overflow
class CountInvalidParentheseSpec(unittest.TestCase):
def test_incomplete_parentheses(self):
self.assertEqual(count_invalid_parentheses("(()"), 1)
self.assertEqual(count_invalid_parentheses("(()("), 2)
def test_overflown_close_parentheses(self):
self.assertEqual(count_invalid_parentheses("()))"), 2)
self.assertEqual(count_invalid_parentheses(")()("), 2)
def test_valid_parentheses(self):
self.assertEqual(count_invalid_parentheses("((()))"), 0)
self.assertEqual(count_invalid_parentheses("()()()"), 0)
self.assertEqual(count_invalid_parentheses("((())(()))"), 0)
self.assertEqual(count_invalid_parentheses(""), 0)
if __name__ == '__main__':
unittest.main(exit=False)
June 20, 2019 [Medium] Integer Exponentiation
Question: Implement integer exponentiation. That is, implement the pow(x, y) function, where x and y are integers and returns x^y.
Do this faster than the naive method of repeated multiplication.
For example, pow(2, 10) should return 1024.
Recursive Solution: https://repl.it/@trsong/Integer-Exponentiation
import unittest
def pow(x, y):
if y == 0:
return 1
elif y < 0:
return pow(1.0 / x, -y)
elif y % 2 == 0:
return pow(x * x, y/2)
else:
return x * pow(x, y-1)
class PowSpec(unittest.TestCase):
def test_power_of_zero(self):
self.assertAlmostEqual(pow(-2, 0), 1)
self.assertAlmostEqual(pow(3, 0), 1)
self.assertAlmostEqual(pow(0, 0), 1)
self.assertAlmostEqual(pow(0.5, 0), 1)
self.assertAlmostEqual(pow(0.6, 0), 1)
def test_negative_power(self):
self.assertAlmostEqual(pow(-2, -2), 0.25)
self.assertAlmostEqual(pow(0.5, -2), 4)
self.assertAlmostEqual(pow(3, -3), 1.0/27)
def test_positive_power(self):
self.assertAlmostEqual(pow(-2, 2), 4)
self.assertAlmostEqual(pow(2, 10), 1024)
self.assertAlmostEqual(pow(-0.5, 2), 0.25)
self.assertAlmostEqual(pow(-2, -9), -1.0/512)
if __name__ == '__main__':
unittest.main(exit=False)
June 19, 2019 LC 289 [Medium] Conway’s Game of Life
Question: Conway’s Game of Life takes place on an infinite two-dimensional board of square cells. Each cell is either dead or alive, and at each tick, the following rules apply:
- Any live cell with less than two live neighbours dies.
- Any live cell with two or three live neighbours remains living.
- Any live cell with more than three live neighbours dies.
- Any dead cell with exactly three live neighbours becomes a live cell.
- A cell neighbours another cell if it is horizontally, vertically, or diagonally adjacent.
Implement Conway’s Game of Life. It should be able to be initialized with a starting list of live cell coordinates and the number of steps it should run for. Once initialized, it should print out the board state at each step. Since it’s an infinite board, print out only the relevant coordinates, i.e. from the top-leftmost live cell to bottom-rightmost live cell.
You can represent a live cell with an asterisk (*) and a dead cell with a dot (.).
My thoughts: The major difficulty comes from the grid being infinite. Usually, when a grid’s size is fixed, we can always use a different grid as a buffer to temporarily hold the result. However, as the grid being infinite, we can only store existing alive cells, and we have to do that in-place so as not to affect the state of neighbor while we process the current cell. And the way to achieve that is that we can create a list to store the changeset. And once we finish generating the changeset, we can then apply the changeset on top of the grid.
Grid Solution with Hashmap and Set: https://repl.it/@trsong/Conways-Game-of-Life
import unittest
class ConwaysGameOfLife(object):
def __init__(self, initial_life_coordinates):
self._grid = {}
self._reset_boundary()
for coord in initial_life_coordinates:
if coord[0] not in self._grid:
self._grid[coord[0]] = set()
self._grid[coord[0]].add(coord[1])
self._update_boundary(coord)
def _reset_boundary(self):
self._left_boundary = None
self._right_boundary = None
self._top_boundary = None
self._bottom_boundary = None
def _update_boundary(self, coord):
self._left_boundary = coord[1] if self._left_boundary is None else min(self._left_boundary, coord[1])
self._right_boundary = coord[1] if self._right_boundary is None else max(self._right_boundary, coord[1])
self._top_boundary = coord[0] if self._top_boundary is None else min(self._top_boundary, coord[0])
self._bottom_boundary = coord[0] if self._bottom_boundary is None else max(self._bottom_boundary, coord[0])
def _check_alive(self, coord):
r, c = coord[0], coord[1]
neighbors = [
[r-1, c-1], [r-1, c], [r-1, c+1],
[r, c-1], [r, c+1],
[r+1, c-1], [r+1, c], [r+1, c+1]
]
num_neighbor = 0
for n in neighbors:
if n[0] in self._grid and n[1] in self._grid[n[0]]:
num_neighbor += 1
is_prev_alive = r in self._grid and c in self._grid[r]
return is_prev_alive and 2 <= num_neighbor <= 3 or not is_prev_alive and num_neighbor == 3
def _next_round(self):
added_changeset = []
removed_changeset = []
for r in xrange(self._top_boundary-1, self._bottom_boundary + 2):
for c in xrange(self._left_boundary-1, self._right_boundary + 2):
is_prev_alive = r in self._grid and c in self._grid[r]
is_now_alive = self._check_alive([r, c])
if not is_prev_alive and is_now_alive:
added_changeset.append([r, c])
elif is_prev_alive and not is_now_alive:
removed_changeset.append([r, c])
for coord in removed_changeset:
self._grid[coord[0]].remove(coord[1])
if not len(self._grid[coord[0]]):
del self._grid[coord[0]]
for coord in added_changeset:
if coord[0] not in self._grid:
self._grid[coord[0]] = set()
self._grid[coord[0]].add(coord[1])
self._reset_boundary()
for r in self._grid:
for c in self._grid[r]:
self._update_boundary([r, c])
def proceed(self, n_round):
for _ in xrange(n_round):
self._next_round()
def display_grid(self):
if not self._grid: return []
res = []
for r in xrange(self._top_boundary, self._bottom_boundary + 1):
if r in self._grid:
line = []
for c in xrange(self._left_boundary, self._right_boundary + 1):
if c in self._grid[r]:
line.append("*")
else:
line.append(".")
res.append("".join(line))
else:
res.append("." * (self._right_boundary - self._left_boundary + 1))
return res
class ConwaysGameOfLifeSpec(unittest.TestCase):
def test_still_lives_scenario(self):
game = ConwaysGameOfLife([[1, 1], [1, 2], [2, 1], [2, 2]])
self.assertEqual(game.display_grid(), [
"**",
"**"
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
"**",
"**"
])
game2 = ConwaysGameOfLife([[0, 1], [0, 2], [1, 0], [1, 3], [2, 1], [2, 2]])
self.assertEqual(game2.display_grid(), [
".**.",
"*..*",
".**."
])
game2.proceed(2)
self.assertEqual(game2.display_grid(), [
".**.",
"*..*",
".**."
])
def test_oscillators_scenario(self):
game = ConwaysGameOfLife([[-100, 0], [-100, 1], [-100, 2]])
self.assertEqual(game.display_grid(), [
"***",
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
"*",
"*",
"*"
])
game.proceed(3)
self.assertEqual(game.display_grid(), [
"***",
])
game2 = ConwaysGameOfLife([[0, 0], [0, 1], [1, 0], [2, 3], [3, 2], [3, 3]])
self.assertEqual(game2.display_grid(), [
"**..",
"*...",
"...*",
"..**"
])
game2.proceed(1)
self.assertEqual(game2.display_grid(), [
"**..",
"**..",
"..**",
"..**",
])
game2.proceed(3)
self.assertEqual(game2.display_grid(), [
"**..",
"*...",
"...*",
"..**"
])
def test_spaceships_scenario(self):
game = ConwaysGameOfLife([[0, 2], [1, 0], [1, 2], [2, 1], [2, 2]])
self.assertEqual(game.display_grid(), [
"..*",
"*.*",
".**"
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
"*..",
".**",
"**."
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
".*.",
"..*",
"***"
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
"*.*",
".**",
".*."
])
game.proceed(1)
self.assertEqual(game.display_grid(), [
"..*",
"*.*",
".**"
])
if __name__ == '__main__':
unittest.main(exit=False)
June 18, 2019 [Medium] Number of Moves on a Grid
Question: There is an N by M matrix of zeroes. Given N and M, write a function to count the number of ways of starting at the top-left corner and getting to the bottom-right corner. You can only move right or down.
For example, given a 2 by 2 matrix, you should return 2, since there are two ways to get to the bottom-right:
- Right, then down
- Down, then right
Given a 5 by 5 matrix, there are 70 ways to get to the bottom-right.
DP Solution: https://repl.it/@trsong/Number-of-Moves-on-a-Grid
import unittest
def calc_num_moves(grid_height, grid_width):
if not grid_height or not grid_width: return 0
# Let dp[i][j] represents total number of moves from 0,0 to i,j
# dp[i][j] = dp[i-1][j] + dp[i][j-1]
dp = [[0 for _ in xrange(grid_width)] for _ in xrange(grid_height)]
for col in xrange(grid_width):
dp[0][col] = 1
for row in xrange(grid_height):
dp[row][0] = 1
for row in xrange(1, grid_height):
for col in xrange(1, grid_width):
dp[row][col] = dp[row-1][col] + dp[row][col-1]
return dp[grid_height-1][grid_width-1]
class CalcNumMoveSpec(unittest.TestCase):
def test_size_zero_grid(self):
self.assertEqual(calc_num_moves(0, 0), 0)
self.assertEqual(calc_num_moves(1, 0), 0)
self.assertEqual(calc_num_moves(0, 1), 0)
def test_square_grid(self):
self.assertEqual(calc_num_moves(1, 1), 1)
self.assertEqual(calc_num_moves(3, 3), 6)
self.assertEqual(calc_num_moves(5, 5), 70)
def test_rectangle_grid(self):
self.assertEqual(calc_num_moves(1, 5), 1)
self.assertEqual(calc_num_moves(5, 1), 1)
self.assertEqual(calc_num_moves(2, 3), 3)
self.assertEqual(calc_num_moves(3, 2), 3)
def test_large_grid(self):
self.assertEqual(calc_num_moves(10, 20), 6906900)
self.assertEqual(calc_num_moves(20, 10), 6906900)
self.assertEqual(calc_num_moves(20, 20), 35345263800)
if __name__ == '__main__':
unittest.main(exit=False)
June 17, 2019 [Medium] Multiplication Table
Question: Suppose you have a multiplication table that is N by N. That is, a 2D array where the value at the i-th row and j-th column is (i + 1) * (j + 1) (if 0-indexed) or i * j (if 1-indexed).
Given integers N and X, write a function that returns the number of times X appears as a value in an N by N multiplication table.
For example, given N = 6 and X = 12, you should return 4, since the multiplication table looks like this:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 8 | 12 | 16 | 20 | 24 |
| 5 | 10 | 15 | 20 | 25 | 30 |
| 6 | 12 | 18 | 24 | 30 | 36 |
And there are 4 12’s in the table.
My thoughts: Sometimes, it is against intuitive to solve a grid searching question without using grid searching stategies. But it could happen. As today’s question is just a math problem features integer factorization.
Counting Number Solution: https://repl.it/@trsong/Multiplication-Table
import unittest
import math
def count_number_in_table(N, X):
if X <= 0: return 0
count = 0
sqrt_x = int(math.sqrt(X))
for candidate in xrange(1, sqrt_x + 1):
# Make sure candidate and its coefficient are within range of N
if candidate > N:
break
elif X % candidate == 0 and X / candidate <= N:
count += 2
if sqrt_x <= N and X == sqrt_x * sqrt_x:
# When candidate and its coefficient are the same, we double-count the result. Therefore take it off.
count -= 1
return count
class CountNumberInTableSpec(unittest.TestCase):
def test_target_out_of_boundary(self):
self.assertEqual(count_number_in_table(1, 100), 0)
self.assertEqual(count_number_in_table(2, -100), 0)
def test_target_range_from_N_to_N_Square(self):
self.assertEqual(count_number_in_table(3, 7), 0)
self.assertEqual(count_number_in_table(3, 4), 1)
self.assertEqual(count_number_in_table(3, 6), 2)
def test_target_range_from_Zero_to_N(self):
self.assertEqual(count_number_in_table(4, 0), 0)
self.assertEqual(count_number_in_table(4, 1), 1)
self.assertEqual(count_number_in_table(4, 2), 2)
self.assertEqual(count_number_in_table(4, 3), 2)
self.assertEqual(count_number_in_table(4, 4), 3)
self.assertEqual(count_number_in_table(12, 12), 6)
self.assertEqual(count_number_in_table(27, 25), 3)
if __name__ == '__main__':
unittest.main(exit=False)
June 16, 2019 [Easy] N-th Perfect Number
Question: A number is considered perfect if its digits sum up to exactly 10.
Given a positive integer n, return the n-th perfect number.
For example, given 1, you should return 19. Given 2, you should return 28.
Generate Perfect Number with Separators: https://repl.it/@trsong/N-th-Perfect-Number
def separator_to_number(sep):
# Imagine there are 10 1's and 9 gaps between consecutive 1's to allow us insert the separator.
# The goal is to sum with each area and get the number:
# 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1
# 1 2 3 4 5 6 7 8 9
# Suppose the separator is: 55679, we just sum with each blocks' number separated by separator:
# The number will be 501121.
prev = 10
base = 1
res = 0
while sep > 0:
cur = sep % 10
res += (prev - cur) * base
prev = cur
base *= 10
sep /= 10
res += prev * base
return res
def separator_increment(sep):
# Suppose the separators are at 199, increase it to 200 and further move the separator to 222 so that no later separator can be smaller than 2.
sep += 1
stack = []
while sep > 0:
stack.append(sep % 10)
sep /= 10
res = 0
prev = 0
while stack:
cur = stack.pop()
prev = max(cur, prev)
res = 10 * res + prev
return res
def perfect_number_at(n):
separator = 0
for _ in xrange(n):
separator = separator_increment(separator)
return separator_to_number(separator)
if __name__ == '__main__':
res = [perfect_number_at(x) for x in xrange(1, 51)]
expected = [19, 28, 37, 46, 55, 64, 73, 82, 91, 109, 118, 127, 136, 145, 154, 163, 172, 181, 208, 217, 226, 235, 244, 253, 262, 271, 307, 316, 325, 334, 343, 352, 361, 406, 415, 424, 433, 442, 451, 505, 514, 523, 532, 541, 604, 613, 622, 631, 703, 712]
assert res == expected
June 15, 2019 [Hard] Max Path Value in Directed Graph
Question: In a directed graph, each node is assigned an uppercase letter. We define a path’s value as the number of most frequently-occurring letter along that path. For example, if a path in the graph goes through “ABACA”, the value of the path is 3, since there are 3 occurrences of ‘A’ on the path.
Given a graph with n nodes and m directed edges, return the largest value path of the graph. If the largest value is infinite, then return null.
The graph is represented with a string and an edge list. The i-th character represents the uppercase letter of the i-th node. Each tuple in the edge list (i, j) means there is a directed edge from the i-th node to the j-th node. Self-edges are possible, as well as multi-edges.
For example, the following input graph:
ABACA
[(0, 1),
(0, 2),
(2, 3),
(3, 4)]
Would have maximum value 3 using the path of vertices [0, 2, 3, 4], (A, A, C, A).
The following input graph:
A
[(0, 0)]
Should return null, since we have an infinite loop.
My thoughts: This question is a perfect example illustrates how to apply different teachniques, such as DFS and DP, to solve a graph problem.
The brute force solution is to iterate through all possible vertices and start from where we can search neighbors recursively and find the maximum path value. Which takes O(V * (V + E)).
However, certain nodes will be calculated over and over again. e.g. “AAB”, [(0, 1), (2, 1)] both share same neighbor second A.
Thus, in order to speed up, we can use DP to cache the intermediate result. Let path_value[v][letter] represents the path value starts from v with the letter. Then path_value[v][letter] = max of all path_value[neighbor][letter] And if letter happen to be the current letter, path_value[v][letter] += 1. With DP solution, the time complexity drop to O(V + E).
Solution with DFS and DP: https://repl.it/@trsong/Max-Path-Value-in-Directed-Graph
import unittest
class LetterVertexDirectedGraph(object):
class VertexState(object):
UNVISITED = 0
VISITING = 1
VISITED = 2
def __init__(self, vertex_letters, paths):
self._vertex_letters = vertex_letters
n = len(vertex_letters)
self._neighbor =[[] for _ in xrange(n)]
for edge in paths:
self._neighbor[edge[0]].append(edge[1])
self._state = [self.VertexState.UNVISITED for _ in xrange(n)]
# Let path_value[v][letter] represents the path value starts from v with the letter
self._path_value = [[0 for _ in xrange(26)] for _ in xrange(n)]
def _DFS_found_cycle(self, current):
if self._state[current] == self.VertexState.VISITED:
return False
elif self._state[current] == self.VertexState.VISITING:
# Found a back edge which can be used to form a cycle
return True
self._state[current] = self.VertexState.VISITING
for v in self._neighbor[current]:
if self._DFS_found_cycle(v):
return True
for letter in xrange(26):
# for current letter, path value inherits from max path value from neighbor
self._path_value[current][letter] = max(self._path_value[current][letter], self._path_value[v][letter])
current_letter = self._vertex_letters[current]
self._path_value[current][ord(current_letter) - ord('A')] += 1
self._state[current] = self.VertexState.VISITED
def max_path_value(self):
res = 0
for v in xrange(len(self._vertex_letters)):
if self._DFS_found_cycle(v):
return None
for letter in xrange(26):
res = max(res, self._path_value[v][letter])
return res
class LetterVertexDirectedGraphSpec(unittest.TestCase):
def test_graph_with_self_edge(self):
g = LetterVertexDirectedGraph('A', [(0, 0)])
self.assertIsNone(g.max_path_value())
def test_sample_graph(self):
g = LetterVertexDirectedGraph('ABACA', [
(0, 1), (0, 2), (2, 3), (3, 4)
])
self.assertEqual(g.max_path_value(), 3)
def test_graph_with_cycle(self):
g = LetterVertexDirectedGraph('XZYABC', [
(0, 1), (1, 2), (2, 0), (3, 2), (4, 3), (5, 3)
])
self.assertIsNone(g.max_path_value())
def test_graph_with_disconnected_components(self):
g = LetterVertexDirectedGraph('AABBB', [
(0, 1), (2, 3), (3, 4)
])
self.assertEqual(g.max_path_value(), 3)
def test_complicated_graph(self):
g = LetterVertexDirectedGraph('XZYZYZYZQX', [
(0, 1), (0, 9), (1, 9), (1, 3), (1, 5), (3, 5), (3, 4),
(5, 4), (5, 7), (1, 7), (2, 4), (2, 6), (2, 8), (9, 8)
])
self.assertEqual(g.max_path_value(), 4)
if __name__ == '__main__':
unittest.main(exit=False)
June 14, 2019 [Easy] Largest Product of Three
Question: Given a list of integers, return the largest product that can be made by multiplying any three integers.
For example, if the list is
[-10, -10, 5, 2], we should return 500, since that’s-10 * -10 * 5.You can assume the list has at least three integers.
My thoughts: The largest product of three comes from either max1 * max2 * max3 or min1 * min2 * max1 where min1 is 1st min, max1 is 1st max, vice versa for max2, max3 and min2.
Python Solution: https://repl.it/@trsong/Largest-Product-of-Three
import unittest
from queue import PriorityQueue
def max_3product(nums):
min_queue = PriorityQueue() # stores 1st, 2nd and 3rd max
max_queue = PriorityQueue() # stores 1st, 2nd and 3rd min
for i in xrange(3):
min_queue.put(nums[i])
max_queue.put(-nums[i])
for i in xrange(3, len(nums)):
num = nums[i]
if min_queue.queue[0] < num:
min_queue.put(num)
min_queue.get()
elif -max_queue.queue[0] > num:
max_queue.put(-num)
max_queue.get()
max3 = min_queue.get()
max2 = min_queue.get()
max1 = min_queue.get()
max_queue.get()
min2 = -max_queue.get()
min1 = -max_queue.get()
return max(max1 * max2 * max3, min1 * min2 * max1)
class Max3ProductSpec(unittest.TestCase):
def test_all_positive(self):
self.assertEqual(max_3product([1, 2, 3, 4, 5]), 60)
self.assertEqual(max_3product([2, 3, 6, 1, 1, 6, 3, 2, 1, 6]), 216)
def test_all_negative(self):
self.assertEqual(max_3product([-5, -4, -3, -2, -1]), -6)
self.assertEqual(max_3product([-1, -5, -2, -4, -3]), -6)
self.assertEqual(max_3product([-10, -3, -5, -6, -20]), -90)
def test_mixed(self):
self.assertEqual(max_3product([-1, -1, -1, 0, 2, 3]), 3)
self.assertEqual(max_3product([0, -1, -2, -3, 0]), 0)
self.assertEqual(max_3product([1, -4, 3, -6, 7, 0]), 168)
if __name__ == '__main__':
unittest.main(exit=False)
June 13, 2019 [Medium] Forward DNS Look Up Cache
Question: Forward DNS look up is getting IP address for a given domain name typed in the web browser. e.g. Given “www.samsung.com” should return “107.108.11.123”
The cache should do the following operations:
- Add a mapping from URL to IP address
- Find IP address for a given URL.
Note:
- You can assume all domain name contains only lowercase characters
Hint:
- The idea is to store URLs in Trie nodes and store the corresponding IP address in last or leaf node.
My thoughts: The cahce can also be implemented using hash map; however, trie still has best worse case running time O(n) where n is the length of url. The only drawback of Trie is that it is not so memory efficient.
Trie Solution: https://repl.it/@trsong/Forward-DNS-Look-Up-Cache
import unittest
class TrieNode(object):
def __init__(self, ip=None, children=None):
self.ip = ip
self._children = children
def get_children(self, index):
if not self._children:
self._children = [None] * 27
if not self._children[index]:
self._children[index] = TrieNode()
return self._children[index]
class ForwardDNSCache(object):
def __init__(self):
self._root = TrieNode()
@staticmethod
def char_encode(c):
return ord(c) - ord('a') if c != '.' else 26
def insert(self, url, ip):
cur = self._root
for c in url:
cur = cur.get_children(ForwardDNSCache.char_encode(c))
cur.ip = ip
def search(self, url):
cur = self._root
for c in url:
if not cur:
return None
else:
cur = cur.get_children(ForwardDNSCache.char_encode(c))
if cur:
return cur.ip
else:
return None
class ForwardDNSCacheSpec(unittest.TestCase):
def setUp(self):
self.cache = ForwardDNSCache()
def test_fail_to_get_out_of_bound_result(self):
self.assertIsNone(self.cache.search("www.google.ca"))
self.cache.insert("www.google.com", "1.1.1.1")
self.assertIsNone(self.cache.search("www.google.com.ca"))
def test_result_not_found(self):
self.cache.insert("www.cnn.com", "2.2.2.2")
self.assertIsNone(self.cache.search("www.amazon.ca"))
self.assertIsNone(self.cache.search("www.cnn.ca"))
def test_overwrite_url(self):
self.cache.insert("www.apple.com", "1.2.3.4")
self.assertEqual(self.cache.search("www.apple.com"), "1.2.3.4")
self.cache.insert("www.apple.com", "5.6.7.8")
self.assertEqual(self.cache.search("www.apple.com"), "5.6.7.8")
def test_url_with_same_prefix(self):
self.cache.insert("www.apple.com", "1.2.3.4")
self.cache.insert("www.apple.com.ca", "5.6.7.8")
self.cache.insert("www.apple.com.hk", "9.10.11.12")
self.assertEqual(self.cache.search("www.apple.com"), "1.2.3.4")
self.assertEqual(self.cache.search("www.apple.com.ca"), "5.6.7.8")
self.assertEqual(self.cache.search("www.apple.com.hk"), "9.10.11.12")
def test_non_overlapping_url(self):
self.cache.insert("bilibili.tv", "11.22.33.44")
self.cache.insert("taobao.com", "55.66.77.88")
self.assertEqual(self.cache.search("bilibili.tv"), "11.22.33.44")
self.assertEqual(self.cache.search("taobao.com"), "55.66.77.88")
if __name__ == '__main__':
unittest.main(exit=False)
June 12, 2019 [Hard] RGB Element Array Swap
Question: Given an array of strictly the characters ‘R’, ‘G’, and ‘B’, segregate the values of the array so that all the Rs come first, the Gs come second, and the Bs come last. You can only swap elements of the array.
Do this in linear time and in-place.
For example, given the array
['G', 'B', 'R', 'R', 'B', 'R', 'G'], it should become['R', 'R', 'R', 'G', 'G', 'B', 'B'].
My thoughts: Treat ‘R’,’G’ and ‘B’ as numbers. The problem can be solved by sorting this array based on certain order. We can use Quick Sort to achieve that. And the idea is that we keep three pointers lo <= mid <= hi such that ‘G’ grows from lo, ‘B’ grows from hi and ‘B’ grows from mid and swap w/ lo to make some room. Such technique to partition the array into 3 parts is called 3-Way Quick Select. It feels like normal Quick Select except segregate array into 3 parts.
Solution with 3-Way Quick Select: https://repl.it/@trsong/RGB-Element-Array-Swap
import unittest
def swap_rgb_array(arr):
def swap(i, j):
tmp = arr[i]
arr[i] = arr[j]
arr[j] = tmp
lo = mid = 0
hi = len(arr) - 1
while mid <= hi:
if arr[mid] == 'R':
swap(lo, mid)
lo += 1
mid += 1
elif arr[mid] == 'B':
swap(mid, hi)
hi -= 1
else:
# arr[mid] == 'G'
mid += 1
class SwapRGBArraySpec(unittest.TestCase):
def assert_rbb_swap(self, arr, expected):
swap_rgb_array(arr)
self.assertEqual(arr, expected)
def test_empty_arr(self):
self.assert_rbb_swap([], [])
def test_array_with_two_colors(self):
self.assert_rbb_swap(['R', 'G', 'R', 'G'], ['R', 'R', 'G', 'G'])
self.assert_rbb_swap(['B', 'B', 'G', 'G'], ['G', 'G', 'B', 'B'])
self.assert_rbb_swap(['R', 'B', 'R'], ['R', 'R', 'B'])
def test_array_in_reverse_order(self):
self.assert_rbb_swap(['B', 'B', 'G', 'R', 'R', 'R'], ['R', 'R', 'R', 'G', 'B', 'B'])
self.assert_rbb_swap(['B', 'G', 'R', 'R', 'R', 'R'], ['R', 'R', 'R', 'R', 'G', 'B'])
self.assert_rbb_swap(['B', 'G', 'G', 'G', 'R'], ['R', 'G', 'G', 'G', 'B'])
def test_array_in_sorted_order(self):
arr = ['R', 'R', 'G', 'B', 'B', 'B', 'B']
self.assert_rbb_swap(arr, arr)
def test_array_in_random_order(self):
self.assert_rbb_swap(['B', 'R', 'G', 'G', 'R', 'B'], ['R', 'R', 'G', 'G', 'B', 'B'])
self.assert_rbb_swap(['G', 'B', 'R', 'R', 'B', 'R', 'G'], ['R', 'R', 'R', 'G', 'G', 'B', 'B'])
if __name__ == '__main__':
unittest.main(exit=False)
June 11, 2019 [Easy] Word Search Puzzle
Question: Given a 2D matrix of characters and a target word, write a function that returns whether the word can be found in the matrix by going left-to-right, or up-to-down.
For example, given the following matrix:
[['F', 'A', 'C', 'I'],
['O', 'B', 'Q', 'P'],
['A', 'N', 'O', 'B'],
['M', 'A', 'S', 'S']]
and the target word ‘FOAM’, you should return true, since it’s the leftmost column. Similarly, given the target word ‘MASS’, you should return true, since it’s the last row.
My thoughts: A naive solution is to identify, in the grid, the matching cell of first character of the target word. Then check the remaining character either in left-to-right or up-to-down direction. Which is quite straightforward.
However, I think this might be a good chance to practice KMP Algorithm.
Solution with KMP Algorithm: https://repl.it/@trsong/Word-Search-Puzzle
import unittest
class KMPSearch(object):
def __init__(self, pattern):
self._lps = KMPSearch.computeLPSArray(pattern)
self._pattern = pattern
@staticmethod
def computeLPSArray(pattern):
m = len(pattern)
lps = [0] * m
prev_LPS = 0 # length of the longest prefix suffix
i = 1
while i < m:
if pattern[i] == pattern[prev_LPS]:
prev_LPS += 1
lps[i] = prev_LPS
i += 1
elif prev_LPS > 0:
prev_LPS = lps[prev_LPS - 1]
else:
lps[i] = 0
i += 1
return lps
def search(self, text):
m = len(self._pattern)
n = len(text)
i = j = 0
while i < n:
if self._pattern[j] == text[i]:
i += 1
j += 1
if j == m:
return True
elif i < n and self._pattern[j] != text[i]:
if j > 0:
j = self._lps[j-1]
else:
i += 1
return False
class WordSearchPuzzle(object):
def __init__(self, grid):
self._grid = grid
def contains(self, target):
kmp = KMPSearch(target)
n, m = len(self._grid), len(self._grid[0])
for r in xrange(n):
if kmp.search(self._grid[r]):
return True
for c in xrange(m):
if kmp.search([self._grid[r][c] for r in xrange(n)]):
return True
return False
class WordSearchPuzzleSpec(unittest.TestCase):
def test_target_word_overflow(self):
puzzle = WordSearchPuzzle([['A']])
self.assertFalse(puzzle.contains("BEE"))
self.assertFalse(puzzle.contains("AQUA"))
self.assertFalse(puzzle.contains("AA"))
self.assertTrue(puzzle.contains("A"))
def test_target_word_on_boundary(self):
puzzle = WordSearchPuzzle([
['A', 'C', 'E', 'R'],
['L', 'I', 'S', 'T'],
['L', 'I', 'P', 'S']
])
self.assertTrue(puzzle.contains("ALL"))
self.assertTrue(puzzle.contains("AL"))
self.assertTrue(puzzle.contains("ACE"))
self.assertTrue(puzzle.contains("ACER"))
self.assertTrue(puzzle.contains("RTS"))
self.assertTrue(puzzle.contains("LIPS"))
self.assertTrue(puzzle.contains("LIST"))
self.assertTrue(puzzle.contains("ST"))
self.assertFalse(puzzle.contains("LA"))
self.assertFalse(puzzle.contains("RE"))
self.assertFalse(puzzle.contains("PI"))
self.assertFalse(puzzle.contains("CSS"))
self.assertFalse(puzzle.contains("ET"))
def test_square_grid(self):
puzzle = WordSearchPuzzle([
['F', 'A', 'C', 'I'],
['O', 'B', 'Q', 'P'],
['A', 'N', 'O', 'B'],
['M', 'A', 'S', 'S']
])
self.assertTrue(puzzle.contains("FOAM"))
self.assertTrue(puzzle.contains("MASS"))
self.assertTrue(puzzle.contains("NO"))
self.assertTrue(puzzle.contains("OS"))
self.assertTrue(puzzle.contains("IP"))
def test_grid_with_duplicates(self):
puzzle = WordSearchPuzzle([
['A', 'B', 'A', 'B', 'A', 'B', 'A', 'B', 'C', 'A']
])
self.assertTrue(puzzle.contains("ABABABCA"))
self.assertFalse(puzzle.contains("BABACA"))
self.assertFalse(puzzle.contains("BACA"))
self.assertTrue(puzzle.contains("BABC"))
self.assertTrue(puzzle.contains("BABA"))
if __name__ == '__main__':
unittest.main(exit=False)
June 10, 2019 [Medium] Locking in Binary Tree
Question: Implement locking in a binary tree. A binary tree node can be locked or unlocked only if all of its descendants or ancestors are not locked.
Design a binary tree node class with the following methods:
is_locked, which returns whether the node is lockedlock, which attempts to lock the node. If it cannot be locked, then it should return false. Otherwise, it should lock it and return true.unlock, which unlocks the node. If it cannot be unlocked, then it should return false. Otherwise, it should unlock it and return true.You may augment the node to add parent pointers or any other property you would like. You may assume the class is used in a single-threaded program, so there is no need for actual locks or mutexes. Each method should run in O(h), where h is the height of the tree.
My thoughts: Whether we can successfully lock or unlock a binary tree node depends on if there exist a locked node above or below. So in order to efficiently calculate has_locked_above() and has_locked_below() we can augment the original BasicTreeNode with reference to parent and a counter which stores the number of locked node below. Doing such can allow running time of lock() and unlock() to be O(h).
Python Solution: https://repl.it/@trsong/Locking-in-Binary-Tree
import unittest
class BasicTreeNode(object):
def __init__(self, left=None, right=None):
self.left = left
self.right = right
self._locked = False
class TreeNode(BasicTreeNode):
def __init__(self, left=None, right=None):
BasicTreeNode.__init__(self, left, right)
self._num_locked_below = 0
self._parent = None
if self.left:
self.left._parent = self
if self.right:
self.right._parent = self
def _has_lock_below(self):
return self._num_locked_below > 0
def _has_lock_above(self):
node = self._parent
while node:
if node._locked:
return True
node = node._parent
return False
def _can_lock(self):
return not (self.is_locked() or self._has_lock_above() or self._has_lock_below())
def _can_unlock(self):
return self.is_locked() and not self._has_lock_above() and not self._has_lock_below()
def _update_lock_count(self, diff):
node = self._parent
while node:
node._num_locked_below += diff
node = node._parent
def is_locked(self):
return self._locked
def lock(self):
if self._can_lock():
self._locked = True
self._update_lock_count(1)
return True
return False
def unlock(self):
if self._can_unlock():
self._locked = False
self._update_lock_count(-1)
return True
return False
class TreeNodeSpec(unittest.TestCase):
def setUp(self):
"""
a
/ \
b c
/ \ / \
d e f g
"""
self.d = TreeNode()
self.e = TreeNode()
self.f = TreeNode()
self.g = TreeNode()
self.b = TreeNode(self.d, self.e)
self.c = TreeNode(self.f, self.g)
self.a = TreeNode(self.b, self.c)
def assert_lock_node(self, node):
self.assertIsNotNone(node)
self.assertFalse(node.is_locked())
self.assertTrue(node.lock())
self.assertTrue(node.is_locked())
def assert_unlock_node(self, node):
self.assertIsNotNone(node)
self.assertTrue(node.is_locked())
self.assertTrue(node.unlock())
self.assertFalse(node.is_locked())
def test_non_overlapping_lock(self):
self.assert_lock_node(self.b)
self.assert_lock_node(self.f)
self.assert_lock_node(self.g)
self.assert_unlock_node(self.b)
self.assert_unlock_node(self.f)
self.assert_unlock_node(self.g)
def test_has_lock_above(self):
self.assert_lock_node(self.a)
self.assertFalse(self.b.is_locked())
self.assertFalse(self.b.lock())
self.assert_unlock_node(self.a)
self.assert_lock_node(self.b)
def test_has_lock_below(self):
self.assert_lock_node(self.e)
self.assertFalse(self.a.lock())
self.assertFalse(self.b.lock())
self.assert_unlock_node(self.e)
self.assert_lock_node(self.b)
if __name__ == '__main__':
unittest.main(exit=False)
June 9, 2019 [Medium] Searching in Rotated Array
Question: A sorted array of integers was rotated an unknown number of times. Given such an array, find the index of the element in the array in faster than linear time. If the element doesn’t exist in the array, return null.
For example, given the array
[13, 18, 25, 2, 8, 10]and the element 8, return 4 (the index of 8 in the array).You can assume all the integers in the array are unique.
My thoughts: In order to solve this problem, we will need the following properties:
- Multiple rotation can at most break array into two sorted subarrays.
- All numbers on left sorted subarray are always larger than numbers on the right sorted subarray.
For property 1, we can use some example. Suppose input array is [1, 2, 3, 4, 5, 6] and rotating once gives [4, 5, 6, 1, 2, 3]. And rotate it again will give [6, 1, 2, 3, 4, 5]. And if we rotate it one more time can give [3, 4, 5, 6, 1, 2] - still two sorted subarrays.
For property 2, think about breaking the input array into left and right part. i.e. array = left + right. After rotation it looks like rotated_array = right + left. Any number on right will be greater than number on left.
Which one will you choose? One Binary Search vs Two
A lot of people think binary search is about checking if arr[mid] against target number. That’s why people are thinking about split the array into two sorted parts and searching target separately on each of them. Yet doing such need to perform binary searching twice:
- Use binary search to find the cutoff index such that left part and right part both are sorted.
- Either binary search on left part or right part.
However, ONE binary search should be sufficient for this question as the idea of binary search is about how to breaking the problem size into half instead of checking arr[mid] against target number. Two edge cases could happen while doing binary search:
- mid element is on the same part as the left-most element
- mid element is on different part
Binary Search Solution: https://repl.it/@trsong/Search-in-Rotated-Array
import unittest
def rotated_array_search(nums, target):
if not nums: return None
lo = 0
hi = len(nums) - 1
while lo <= hi:
mid = lo + (hi - lo) / 2
if nums[mid] == target:
return mid
elif nums[lo] < nums[mid] and nums[mid] < target or nums[lo] > target:
lo = mid + 1
else:
hi = mid - 1
return None
class RotatedArraySearchSpec(unittest.TestCase):
def test_array_without_rotation(self):
self.assertIsNone(rotated_array_search([], 0))
self.assertEqual(rotated_array_search([1, 2, 3], 3), 2)
self.assertIsNone(rotated_array_search([1, 3], 2))
def test_array_with_one_rotation(self):
self.assertIsNone(rotated_array_search([4, 5, 6, 1, 2, 3], 0))
self.assertEqual(rotated_array_search([4, 5, 6, 1, 2, 3], 6), 2)
self.assertEqual(rotated_array_search([13, 18, 25, 2, 8, 10], 8), 4)
def test_array_with_two_rotations(self):
self.assertEqual(rotated_array_search([6, 1, 2, 3, 4, 5], 6), 0)
self.assertEqual(rotated_array_search([5, 6, 1, 2, 3, 4], 3), 4)
if __name__ == '__main__':
unittest.main(exit=False)
June 8, 2019 [Hard] Longest Palindromic Substring
Question: Given a string, find the longest palindromic contiguous substring. If there are more than one with the maximum length, return any one.
For example, the longest palindromic substring of “aabcdcb” is “bcdcb”. The longest palindromic substring of “bananas” is “anana”.
My thoughts: Pick all substrings one by one and validate if the substring w/ cache.
Solution with Cache: https://repl.it/@trsong/Longest-Palindromic-Substring
import unittest
def find_palindrome(word):
n = len(word)
max_delta = 0
start = 0
cache = [[None for _ in xrange(n)] for _ in xrange(n)]
for delta in xrange(n):
for s in xrange(n - delta):
if is_palindrome(word, s, s + delta, cache):
start = s
max_delta = delta
return word[start: start + max_delta + 1]
def is_palindrome(word, i, j, cache):
if i >= j:
return True
if cache[i][j] is None:
if word[i] != word[j]:
cache[i][j] = False
else:
cache[i][j] = is_palindrome(word, i+1, j-1, cache)
return cache[i][j]
class FindPalindromeSpec(unittest.TestCase):
def test_one_letter_palindrome(self):
word = "abcdef"
result = find_palindrome(word)
self.assertTrue(result in word and len(result) == 1)
def test_multiple_length_2_palindrome(self):
result = find_palindrome("zaaqrebbqreccqreddz")
self.assertTrue(result in ["aa", "bb", "cc", "dd"])
def test_multiple_length_3_palindrome(self):
result = find_palindrome("xxaza1xttv1xpqp1x")
self.assertTrue(result in ["aza", "ttt", "pqp"])
def test_sample_palindrome(self):
self.assertEqual(find_palindrome("aabcdcb"), "bcdcb")
self.assertEqual(find_palindrome("bananas"), "anana")
if __name__ == '__main__':
unittest.main(exit=False)
Note, Longest Palindromic Substring can be efficiently solved using Manacher’s Algorithm. Example of how it works: http://manacher-viz.s3-website-us-east-1.amazonaws.com/#/
Linear Solution with Manacher’s Algorithm: https://repl.it/@trsong/Longest-Palindromic-Substring-with-Manachers-Algorithm
def manacher(s0):
T = '$#' + '#'.join(s0) + '#@'
l = len(T)
P = [0] * l
R, C = 0, 0
for i in range(1,l-1):
if i < R:
P[i] = min(P[2 * C - i], R - i)
while T[i+(P[i]+1)] == T[i-(P[i]+1)]:
P[i] += 1
if P[i] + i > R:
R = P[i] + i
C = i
return P
def find_palindrome(word):
P = manacher(word)
maxLen = 0;
centerIndex = 0;
for i in xrange(1, len(P)):
if P[i] > maxLen:
maxLen = P[i]
centerIndex = i
start = (centerIndex - maxLen) / 2
return word[start: start + maxLen]
June 7, 2019 [Medium] K Color Problem
Question: Given an undirected graph represented as an adjacency matrix and an integer k, write a function to determine whether each vertex in the graph can be colored such that no two adjacent vertices share the same color using at most k colors.
My thoughts: Solve this problem with backtracking. For each node, testing all colors one-by-one; if it turns out there is something wrong with current color, we will backtrack to test other colors.
Backtracking Solution: https://repl.it/@trsong/K-Color-Problem
import unittest
def exist_k_color_solution_helper_recur(remaining, neighbors, k, colors):
if not remaining: return True
current = remaining[0]
current_neighbors = [i for i in xrange(len(neighbors)) if neighbors[current][i]]
for c in xrange(k):
# If any neighbor of current has same color as current, then we move onto next color
if any(colors[node] == c for node in current_neighbors):
continue
colors[current] = c
if exist_k_color_solution_helper_recur(remaining[1:], neighbors, k, colors):
return True
colors[current] = None
return False
def exist_k_color_solution(neighbors, k):
colors = [None] * len(neighbors)
remaining = range(len(neighbors))
return exist_k_color_solution_helper_recur(remaining, neighbors, k, colors)
class KColorProblemSpec(unittest.TestCase):
@staticmethod
def generateCompleteGraph(n):
return [[1 if i != j else 0 for i in xrange(n)] for j in xrange(n)]
def test_k2_graph(self):
k2 = KColorProblemSpec.generateCompleteGraph(2)
self.assertFalse(exist_k_color_solution(k2, 1))
self.assertTrue(exist_k_color_solution(k2, 2))
self.assertTrue(exist_k_color_solution(k2, 3))
def test_k3_graph(self):
k3 = KColorProblemSpec.generateCompleteGraph(3)
self.assertFalse(exist_k_color_solution(k3, 2))
self.assertTrue(exist_k_color_solution(k3, 3))
self.assertTrue(exist_k_color_solution(k3, 4))
def test_k4_graph(self):
k4 = KColorProblemSpec.generateCompleteGraph(4)
self.assertFalse(exist_k_color_solution(k4, 3))
self.assertTrue(exist_k_color_solution(k4, 4))
self.assertTrue(exist_k_color_solution(k4, 5))
def test_square_graph(self):
square = [
[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]
]
self.assertFalse(exist_k_color_solution(square, 1))
self.assertTrue(exist_k_color_solution(square, 2))
self.assertTrue(exist_k_color_solution(square, 3))
def test_star_graph(self):
star = [
[0, 0, 1, 1, 0],
[0, 0, 0, 1, 1],
[1, 0, 0, 0, 1],
[1, 1, 0, 0, 0],
[0, 1, 1, 0, 0]
]
self.assertFalse(exist_k_color_solution(star, 2))
self.assertTrue(exist_k_color_solution(star, 3))
self.assertTrue(exist_k_color_solution(star, 4))
def test_disconnected_graph(self):
disconnected = [[0 for _ in xrange(10)] for _ in xrange(10)]
self.assertTrue(exist_k_color_solution(disconnected, 1))
if __name__ == '__main__':
unittest.main(exit=False)
June 6, 2019 [Medium] Craft Sentence
Question: Write an algorithm to justify text. Given a sequence of words and an integer line length k, return a list of strings which represents each line, fully justified.
More specifically, you should have as many words as possible in each line. There should be at least one space between each word. Pad extra spaces when necessary so that each line has exactly length k. Spaces should be distributed as equally as possible, with the extra spaces, if any, distributed starting from the left.
If you can only fit one word on a line, then you should pad the right-hand side with spaces.
Each word is guaranteed not to be longer than k.
For example, given the list of words ["the", "quick", "brown", "fox", "jumps", "over", "the", "lazy", "dog"] and k = 16, you should return the following:
["the quick brown",
"fox jumps over",
"the lazy dog"]
My thoughts: Try to fit as many words as possible in order to find the maximum number of word we can fit into each line. Then determine the base number of spaces each gap can fit as well as extra space each space might be able to fit.
Python Solution: https://repl.it/@trsong/Craft-Sentence
import unittest
def craft_sentence(words, k):
index = 0
n = len(words)
res = []
while index < n:
end = index + 1
# try to fit as many words as possible to find max word it can be fit
remain = k - len(words[index])
while end < n and remain > len(words[end]):
remain -= 1 + len(words[end])
end += 1
num_words = end - index
line = [words[index]]
if num_words == 1:
line.append(" " * remain)
else:
num_gap = num_words - 1
extra_space = remain / num_gap
pad_until = remain % num_gap
for j in xrange(1, num_words):
num_space = 1 + extra_space + (1 if j <= pad_until else 0)
line.append(" " * num_space)
line.append(words[index + j])
res.append("".join(line))
index = end
return res
class CraftSentenceSpec(unittest.TestCase):
def test_fit_only_one_word(self):
self.assertEqual(craft_sentence(["test", "same", "length", "string"], 7), ["test ", "same ", "length ", "string "])
self.assertEqual(craft_sentence(["test", "same", "length", "string"], 6), ["test ", "same ", "length", "string"])
self.assertEqual(craft_sentence(["to", "be"], 2), ["to", "be"])
def test_fit_two_words(self):
self.assertEqual(craft_sentence(["To", "be", "or", "not", "to", "be"], 6), ["To be", "or not", "to be"])
self.assertEqual(craft_sentence(["Greed", "is", "not", "good"], 11), ["Greed is", "not good"])
def test_fit_more_words(self):
self.assertEqual(craft_sentence(["the", "quick", "brown", "fox", "jumps", "over", "the", "lazy", "dog"], 16), ["the quick brown", "fox jumps over", "the lazy dog"])
if __name__ == '__main__':
unittest.main(exit=False)
June 5, 2019 [Medium] Break Sentence
Question: Given a string s and an integer k, break up the string into multiple lines such that each line has a length of k or less. You must break it up so that words don’t break across lines. Each line has to have the maximum possible amount of words. If there’s no way to break the text up, then return null.
You can assume that there are no spaces at the ends of the string and that there is exactly one space between each word.
For example, given the string “the quick brown fox jumps over the lazy dog” and
k = 10, you should return:["the quick", "brown fox", "jumps over", "the lazy", "dog"]. No string in the list has a length of more than 10.
Python Solution: https://repl.it/@trsong/Break-Sentence
import unittest
def break_sentence(sentence, k):
if not sentence or k <= 0: return None
res = []
i = 0
n = len(sentence)
while i < n:
end = i + k
while i < end < n and sentence[end] != " ":
end -= 1
if end <= i:
return None
res.append(sentence[i: end])
i = end + 1
return res
class BreakSentenceSpec(unittest.TestCase):
def test_empty_sentence(self):
self.assertEqual(break_sentence("", 0), None)
self.assertEqual(break_sentence("", 1), None)
def test_sentence_with_unbreakable_words(self):
self.assertEqual(break_sentence("How do you turn this on", 3), None)
self.assertEqual(break_sentence("Internationalization", 10), None)
def test_window_fit_one_word(self):
self.assertEqual(break_sentence("Banana Leaf", 7), ["Banana", "Leaf"])
self.assertEqual(break_sentence("Banana Leaf", 6), ["Banana", "Leaf"])
self.assertEqual(break_sentence("Ebi Ten", 5), ["Ebi", "Ten"])
def test_window_fit_more_than_two_words(self):
self.assertEqual(break_sentence("Cheese Steak Jimmy's", 12), ["Cheese Steak", "Jimmy's"])
self.assertEqual(break_sentence("I see dead people", 10), ["I see dead", "people"])
self.assertEqual(break_sentence("See no evil. Hear no evil. Speak no evil.", 14), ["See no evil.", "Hear no evil.", "Speak no evil."])
self.assertEqual(break_sentence("the quick brown fox jumps over the lazy dog", 10), ["the quick", "brown fox", "jumps over", "the lazy", "dog"])
self.assertEqual(break_sentence("To be or not to be", 1000), ["To be or not to be"])
if __name__ == '__main__':
unittest.main(exit=False)
June 4, 2019 [Easy] Sell Stock
Question: Given an array of numbers representing the stock prices of a company in chronological order, write a function that calculates the maximum profit you could have made from buying and selling that stock once. You must buy before you can sell it.
For example, given
[9, 11, 8, 5, 7, 10], you should return 5, since you could buy the stock at 5 dollars and sell it at 10 dollars.
Python Solution: https://repl.it/@trsong/Sell-Stock
import unittest
def max_profit(stock_data):
if not stock_data: return 0
min_so_far = stock_data[0]
max_profit = 0
for price in stock_data:
if price < min_so_far:
min_so_far = price
else:
max_profit = max(max_profit, price - min_so_far)
return max_profit
class MaxProfitSpec(unittest.TestCase):
def test_blank_data(self):
self.assertEqual(max_profit([]), 0)
def test_1_day_data(self):
self.assertEqual(max_profit([9]), 0)
self.assertEqual(max_profit([-1]), 0)
def test_monotonically_increase(self):
self.assertEqual(max_profit([1, 2, 3]), 2)
self.assertEqual(max_profit([1, 1, 1, 2, 2, 3, 3, 3]), 2)
def test_monotonically_decrease(self):
self.assertEqual(max_profit([3, 2, 1]), 0)
self.assertEqual(max_profit([3, 3, 3, 2, 2, 1, 1, 1]), 0)
def test_raise_suddenly(self):
self.assertEqual(max_profit([3, 2, 1, 1, 2]), 1)
self.assertEqual(max_profit([3, 2, 1, 1, 9]), 8)
def test_drop_sharply(self):
self.assertEqual(max_profit([1, 3, 0]), 2)
self.assertEqual(max_profit([1, 3, -1]), 2)
def test_bear_market(self):
self.assertEqual(max_profit([10, 11, 5, 7, 1, 2]), 2)
self.assertEqual(max_profit([10, 11, 1, 4, 2, 7, 5]), 6)
def test_bull_market(self):
self.assertEqual(max_profit([1, 5, 3, 7, 2, 14, 10]), 13)
self.assertEqual(max_profit([5, 1, 11, 10, 12]), 11)
if __name__ == '__main__':
unittest.main(exit=False)
June 3, 2019 LC 352 [Hard] Data Stream as Disjoint Intervals
Question: Given a data stream input of non-negative integers a1, a2, …, an, …, summarize the numbers seen so far as a list of disjoint intervals.
For example, suppose the integers from the data stream are 1, 3, 7, 2, 6, …, then the summary will be:
[1, 1]
[1, 1], [3, 3]
[1, 1], [3, 3], [7, 7]
[1, 3], [7, 7]
[1, 3], [6, 7]
Follow up:
What if there are lots of merges and the number of disjoint intervals are small compared to the data stream’s size?
My thoughts: Using heap to store all intervals. When get intervals, pop element with smallest start time one by one, there are only 3 cases:
- Element Overlapping w/ previous interval, then we do nothing
- Element will update existing interval’s start or end time, then we update the interval
- Element will cause two intervals to merge.
Solution with Heap: https://repl.it/@trsong/Data-Stream-as-Disjoint-Intervals
from queue import PriorityQueue
import unittest
class SummaryRanges(object):
def __init__(self):
self._intervals = PriorityQueue()
self._exist = set()
def add_num(self, val):
if val not in self._exist:
self._intervals.put((val, [val, val]))
self._exist.add(val)
def get_intervals(self):
if self._intervals.empty(): return []
res = []
while not self._intervals.empty():
interval = self._intervals.get()[1]
if not res:
res.append(interval)
else:
prev = res[-1]
if interval[0] <= prev[1] + 1:
prev[1] = max(prev[1], interval[1])
else:
res.append(interval)
for elem in res:
self._intervals.put((elem[0], elem))
return res
class SummaryRangesSpec(unittest.TestCase):
def setUp(self):
self.sr = SummaryRanges()
def test_sample(self):
self.sr.add_num(1)
self.assertEqual(self.sr.get_intervals(), [[1, 1]])
self.sr.add_num(3)
self.assertEqual(self.sr.get_intervals(), [[1, 1], [3, 3]])
self.sr.add_num(7)
self.assertEqual(self.sr.get_intervals(), [[1, 1], [3, 3], [7, 7]])
self.sr.add_num(2)
self.assertEqual(self.sr.get_intervals(), [[1, 3], [7, 7]])
self.sr.add_num(6)
self.assertEqual(self.sr.get_intervals(), [[1, 3], [6, 7]])
def test_none_overlapping(self):
self.sr.add_num(3)
self.sr.add_num(1)
self.sr.add_num(5)
self.assertEqual(self.sr.get_intervals(), [[1, 1], [3, 3], [5, 5]])
def test_val_in_existing_intervals(self):
self.sr.add_num(3)
self.sr.add_num(2)
self.sr.add_num(1)
self.sr.add_num(5)
self.sr.add_num(6)
self.sr.add_num(7)
self.assertEqual(self.sr.get_intervals(), [[1, 3], [5, 7]])
self.sr.add_num(6)
self.assertEqual(self.sr.get_intervals(), [[1, 3], [5, 7]])
def test_val_join_two_intervals(self):
self.sr.add_num(3)
self.sr.add_num(2)
self.sr.add_num(1)
self.sr.add_num(5)
self.sr.add_num(6)
self.assertEqual(self.sr.get_intervals(), [[1, 3], [5, 6]])
self.sr.add_num(4)
self.assertEqual(self.sr.get_intervals(), [[1, 6]])
if __name__ == '__main__':
unittest.main(exit=False)
Above solution has complexity O(NlogN)
add_numand O(NlogN)get_intervals. We can do better forget_intervalsto make it O(N) by using Interval Search Tree which takes O(logN) to insert and query to overlapping intervals.
class Node:
def __init__(self, val, left=None, right=None)
self.interval = [val, val]
self.max_end = vale # max end in subtree
self.left = left
self.right = right
For add_num, we can query for [val, val] first, if exists. We simply return. Otherwise, we query for [val - 1, val - 1] and [val + 1, val + 1] and determine if we append previous interval w/ val or prepend w/ next interval. If neither of them exists, we simply insert a new interval [val, val].
The result of get_intervals is simply in-order traversal of Interval Search Tree.
TODO tsong: tree rotation to mantain balance is way too complicated during code interview, so omit the detailed implementation.
June 2, 2019 [Hard] Array Shuffle
Question: Given an array, write a program to generate a random permutation of array elements. This question is also asked as “shuffle a deck of cards” or “randomize a given array”. Here shuffle means that every permutation of array element should equally likely.
Input: [1, 2, 3, 4, 5, 6]
Output: [3, 4, 1, 5, 6, 2]
The output can be any random permutation of the input such that all permutation are equally likely.
Hint: Given a function that generates perfectly random numbers between 1 and k (inclusive) where k is an input, write a function that shuffles the input array using only swaps.
My thoughts: It’s quite tricky to figure out how to evenly shuffle an array unless you understand there is no difference between shuffle an array versus randomly generate a permutation of that array.
So, how to randomly generate a permutation of an array? That’s simple. Just imagine you hold a deck of cards on your hand, and each time you randomly draw a card until not more cards available.
| Round | Remaining Cards | Chosen Cards |
|---|---|---|
| 0 | [1, 2, 3, 4, 5] |
[] |
| 1 | [1, 3, 4, 5] |
[2] |
| 2 | [1, 3, 5] |
[4, 2] |
| 3 | [3, 5] |
[1, 4, 2] |
| 4 | [3] |
[5, 1, 4, 2] |
| 1 | [] |
[3, 5, 1, 4, 2] |
It seems we can do that in-place:
| Round | Remaining Cards | Chosen Cards |
|---|---|
| 0 | [1, 2, 3, 4, 5|] |
| 1 | [1, 3, 4, 5 | 2] |
| 2 | [1, 3, 5 | 4, 2] |
| 3 | [3, 5 | 1, 4, 2] |
| 4 | [3 | 5, 1, 4, 2] |
| 1 | [|3, 5, 1, 4, 2] |
Python Solution:https://repl.it/@trsong/Array-Shuffle
from random import randint
def array_shuffle(nums):
for last in xrange(len(nums) - 1, 0, -1):
chosen = randint(0, last)
# move the chosen number to last and move on
nums[chosen], nums[last] = nums[last], nums[chosen]
def print_shuffle_histogram(nums, repeat):
"""Print the frequency of each position get swapped"""
n = len(nums)
original = nums[:]
swap_freq = [0] * n
for _ in xrange(repeat):
array_shuffle(nums)
for i in xrange(n):
if original[i] != nums[i]:
swap_freq[i] += 1
print swap_freq
if __name__ == '__main__':
nums = range(10)
# The frequency map for position get swapped should look like:
# [9010, 9036, 9015, 9035, 9006, 8935, 8990, 8951, 8926, 8985]
# Indicates each postion has same probability to be shuffled
print_shuffle_histogram(nums, repeat=10000)
June 1, 2019 [Easy] Rand7
Question: Given a function
rand5(), use that function to implement a functionrand7()where rand5() returns an integer from 1 to 5 (inclusive) with uniform probability and rand7() is from 1 to 7 (inclusive). Also, use of any other library function and floating point arithmetic are not allowed.
My thoughts: You might ask how is it possible that a random number ranges from 1 to 5 can generate another random number ranges from 1 to 7? Well, think about how binary number works. For example, any number ranges from 0 to 3 can be represents in binary: 00, 01, 10 and 11. Each digit ranges from 0 to 1. Yet it can represents any number. Moreover, all digits are independent which means all number have the same probability to generate.
Just like the idea of a binary system, we can design a quinary (base-5) numeral system. And 2 digits is sufficient: 00, 01, 02, 03, 04, 10, 11, ..., 33, 34, 40, 41, 42, 43, 44. (25 numbers in total) In decimal, “d1d0” base-5 equals 5 * d1 + d0 where d0, d1 ranges from 0 to 4. And entire “d1d0” ranges from 0 to 24. That should be sufficient to cover 1 to 7.
So whenever we get a random number in 1 to 7, we can simply return otherwise replay the same process over and over again until get a random number in 1 to 7.
But, what if rand5 is expensive to call? Can we limit the call to rand5?
Yes, we can. We can just break the interval into the multiple of the modules. eg. [0, 6], [7, 13] and [14, 20]. Once mod 7, all of them will be [0, 6]. And whenever we encounter 21 to 24, we simply discard it and replay the same algorithem mentioned above.
Python Solution: https://repl.it/@trsong/Rand7
from random import randint
def rand5():
return randint(1, 5)
def rand7():
d0 = rand5() - 1 # d0 ranges from [0, 4]
d1 = rand5() - 1 # d1 ranges from [0, 4]
num = 5 * d1 + d0 # num ranges from [0, 24]
if num > 20:
return rand7()
else:
# num can be one of:
# [0, 6]
# [7, 13]
# [14, 20]
return num % 7 + 1 # this ranges from [1, 7]
def print_distribution(func, repeat):
histogram = {}
for _ in xrange(repeat):
res = func()
if res not in histogram:
histogram[res] = 0
histogram[res] += 1
print histogram
def main():
# Distribution looks like {1: 10058, 2: 9977, 3: 10039, 4: 10011, 5: 9977, 6: 9998, 7: 9940}
print_distribution(rand7, repeat=70000)
if __name__ == '__main__':
main(
May 31, 2019 [Easy] Rand25, Rand75
Question: Generate 0 and 1 with 25% and 75% probability Given a function rand50() that returns 0 or 1 with equal probability, write a function that returns 1 with 75% probability and 0 with 25% probability using rand50() only. Minimize the number of calls to rand50() method. Also, use of any other library function and floating point arithmetic are not allowed.
Python Solution: https://repl.it/@trsong/Rand25-Rand75
from random import randint
def rand50():
return randint(0, 1)
def rand25_rand75():
return rand50() | rand50() # bitwise OR operation
def print_distribution(func, repeat):
histogram = {}
for _ in xrange(repeat):
res = func()
if res not in histogram:
histogram[res] = 0
histogram[res] += 1
print histogram
def main():
# Distribution looks like {0: 2520, 1: 7480}
print_distribution(rand25_rand75, repeat=10000)
if __name__ == '__main__':
main()
May 30, 2019 [Medium] K-th Missing Number
Question: Given a sorted without any duplicate integer array, define the missing numbers to be the gap among numbers. Write a function to calculate K-th missing number. If such number does not exist, then return null.
For example, original array:
[2,4,7,8,9,15], within the range defined by original array, all missing numbers are:[3,5,6,10,11,12,13,14]
- the 1st missing number is 3,
- the 2nd missing number is 5,
- the 3rd missing number is 6
My thoughts: An array without any gap must be continuous and should look something like the following:
[0, 1, 2, 3, 4, 5, 6, 7]
[8, 9, 10, 11]
...
Which can be easily verified by using last - first element and check the result against length of array.
Likewise, given any index, treat the element the index refer to as the last element, we can easily the number of missing elements by using the following:
def total_missing_on_left(index):
expect_last_number = nums[0] + index
return nums[index] - expect_last_number
Thus, ever since it’s O(1) to verify the total missing numbers on the left against the k-th missing number, we can always use binary search to shrink the searching space into half.
Tips: do you know the template for binary searching the array with lots of duplicates?
eg. Find the index of first 1 in [0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3].
lo = 0
hi = n - 1
while lo < hi:
mid = lo + (hi - lo) / 2 # avoid overflow in some other language like Java
if arr[mid] < target: # this is the condition. When exit the loop, lo will stop at first element that not statify the condition
lo = mid + 1 # why + 1? lo = (lo + hi) / 2 if hi = lo + 1, we will have lo = (2 * lo + 1) / 2 == lo
else:
hi = mid
return lo
Note: above template will return the index of first element that not statify the condition. e.g. If target == 1, the first elem that >= 1 is 1 at index 3. If target == 2, the first elem that >= 2 is 3 at position 10.
Note, why we need to know above template? Like how does it help to solve this question?
Let’s consider the following case: find_kth_missing_number([3, 4, 8, 9, 10, 11, 12], 2).
[3, 4, 8, 9, 10, 11, 12]
Above source array can be converted to the following total_missing_on_left array:
[0, 0, 3, 3, 3, 3, 3]
Above array represents how many missing numbers are on the left of current element.
Since we are looking at the 2-nd missing number. The first element that not less than target is 3 at position 2. Then using that position we can backtrack to get first element that has 3 missing number on the left is 8. Finally, since 8 has 3 missing number on the left, then we imply that 6 must has 2 missing number on the left which is what we are looking for.
Binary Search Solution: https://repl.it/@trsong/K-th-Missing-Number
import unittest
def find_kth_missing_number(nums, k):
if not nums or k <= 0: return None
def total_missing_on_left(index):
expect_last_number = nums[0] + index
return nums[index] - expect_last_number
n = len(nums)
# just imigine all missing number will form an array with index 1..total_missing_number
if k > total_missing_on_left(n-1): return None
lo = 0
hi = n - 1
while lo < hi:
mid = lo + (hi - lo) / 2
if total_missing_on_left(mid) < k :
lo = mid + 1
else:
hi = mid
delta = total_missing_on_left(lo) - k
return nums[lo] - 1 - delta
class FindKthMissingNumberSpec(unittest.TestCase):
def test_empty_source(self):
self.assertIsNone(find_kth_missing_number([], 0))
self.assertIsNone(find_kth_missing_number([], 1))
def test_missing_number_not_exists(self):
self.assertIsNone(find_kth_missing_number([1, 2, 3], 0))
self.assertIsNone(find_kth_missing_number([1, 2, 3], 1))
self.assertIsNone(find_kth_missing_number([1, 3], 2))
def test_one_gap_in_source(self):
self.assertEqual(find_kth_missing_number([3, 4, 8, 9, 10, 11, 12], 1), 5)
self.assertEqual(find_kth_missing_number([3, 4, 8, 9, 10, 11, 12], 2), 6)
self.assertEqual(find_kth_missing_number([3, 4, 8, 9, 10, 11, 12], 3), 7)
self.assertEqual(find_kth_missing_number([3, 6, 7], 1), 4)
self.assertEqual(find_kth_missing_number([3, 6, 7], 2), 5)
def test_multiple_gap_in_source(self):
sample_case = [2,4,7,8,9,15]
self.assertEqual(find_kth_missing_number(sample_case, 1), 3)
self.assertEqual(find_kth_missing_number(sample_case, 2), 5)
self.assertEqual(find_kth_missing_number(sample_case, 3), 6)
self.assertEqual(find_kth_missing_number(sample_case, 4), 10)
self.assertEqual(find_kth_missing_number(sample_case, 5), 11)
if __name__ == '__main__':
unittest.main(exit=False)
May 29, 2019 [Medium] Pre-order & In-order Binary Tree Traversal
Question: Given pre-order and in-order traversals of a binary tree, write a function to reconstruct the tree.
For example, given the following preorder traversal:
[a, b, d, e, c, f, g]
And the following inorder traversal:
[d, b, e, a, f, c, g]
You should return the following tree:
a
/ \
b c
/ \ / \
d e f g
My thoughts: Inorder traversal follows the order:
Inorder(Left), Current, Inorder(Right)
Whereas preorder (DFS searching order) traversal follows the order:
Current, Preorder(Left), Preorder(Right)
If we further expand the inorder traversal, we will get
Inorder(Left), CURRENT, Inorder(Right)
=>
Inorder(Left2), CURRENT2, Inorder(Right2), CURRENT, Inorder(Right)
And if we further expand the preorder traversal
CURRENT, Preorder(Left), Preorder(Right)
=>
CURRENT, CURRENT2, Preorder(Left2), Preorder(Right2), Preorder(Right)
My takeaway is that let’s fucus on the postion of CURRENT. We can use the preorder to keep going left, left, left, until at a point which is not possible and that point is determined by inorder recursive call.
Python Solution: https://repl.it/@trsong/Pre-order-and-In-order-Binary-Tree-Traversal
import unittest
class TreeNode(object):
def __init__(self, data, left=None, right=None):
self.data = data
self.left = left
self.right = right
def __eq__(self, other):
if not other: return False
return self.data == other.data and self.left == other.left and self.right == other.right
def build_tree(inorder, preorder):
class Context:
# Build a elem to index look up dict
inorder_lookup = dict(zip(inorder, xrange(len(inorder))))
preorder_index = 0
def build_inorder_tree_recur(left, right):
if left > right: return None
current = preorder[Context.preorder_index]
Context.preorder_index += 1
node = TreeNode(current)
middle = Context.inorder_lookup[current]
node.left = build_inorder_tree_recur(left, middle - 1) # keep going left until not possible
node.right = build_inorder_tree_recur(middle + 1, right)
return node
return build_inorder_tree_recur(0, len(preorder) - 1)
class BuildTreeSpec(unittest.TestCase):
def test_empty_tree(self):
self.assertIsNone(build_tree([], []))
def test_sample_tree(self):
"""
a
/ \
b c
/ \ / \
d e f g
"""
preorder = ['a', 'b', 'd', 'e', 'c', 'f', 'g']
inorder = ['d', 'b', 'e', 'a', 'f', 'c', 'g']
b = TreeNode('b', TreeNode('d'), TreeNode('e'))
c = TreeNode('c', TreeNode('f'), TreeNode('g'))
a = TreeNode('a', b, c)
self.assertTrue(build_tree(inorder, preorder) == a)
def test_left_heavy_tree(self):
"""
a
/ \
b c
/
d
"""
preorder = ['a', 'b', 'd', 'c']
inorder = ['d', 'b', 'a', 'c']
b = TreeNode('b', TreeNode('d'))
c = TreeNode('c')
a = TreeNode('a', b, c)
self.assertTrue(build_tree(inorder, preorder) == a)
def test_right_heavy_tree(self):
"""
a
/ \
b c
/ \
f g
"""
preorder = ['a', 'b', 'c', 'f', 'g']
inorder = ['b', 'a', 'f', 'c', 'g']
b = TreeNode('b')
c = TreeNode('c', TreeNode('f'), TreeNode('g'))
a = TreeNode('a', b, c)
self.assertTrue(build_tree(inorder, preorder) == a)
def test_left_only_tree(self):
"""
a
/
b
/
c
"""
preorder = ['a', 'b', 'c']
inorder = ['c', 'b', 'a']
self.assertTrue(build_tree(inorder, preorder) == TreeNode('a', TreeNode('b', TreeNode('c'))))
def test_right_only_tree(self):
"""
a
\
b
\
c
"""
preorder = ['a', 'b', 'c']
inorder = ['a', 'b', 'c']
expected = TreeNode('a', right=TreeNode('b', right=TreeNode('c')))
self.assertTrue(build_tree(inorder, preorder) == expected)
if __name__ == '__main__':
unittest.main(exit=False)
May 28, 2019 [Hard] Subset Sum
Question: Given a list of integers S and a target number k, write a function that returns a subset of S that adds up to k. If such a subset cannot be made, then return null.
Integers can appear more than once in the list. You may assume all numbers in the list are positive.
For example, given S = [12, 1, 61, 5, 9, 2] and k = 24, return [12, 9, 2, 1] since it sums up to 24.
My thoughts: It’s too expensive to check every subsets one by one. What we can do is to divide and conquer this problem.
For each element, we either include it to pursuing for target or not include it:
subset_sum(numbers, target) = subset_sum(numbers[1:], target) or subset_sum(numbers[1:], target - numbers[0])
or derive dp formula from above recursive relation:
dp[target][n] = dp[target][n-1] or dp[target-numbers[n-1]][n-1]
DP Solution Inspired by Yesterday’s Problem: https://repl.it/@trsong/Multiset-Partition
def subset_sum(numbers, target):
n = len(numbers)
# Let dp[sum][n] represent exiting subset of numbers[:n] with sum as sum:
# * dp[sum][n] = dp[sum][n-1] or dp[sum-a[n-1]][n-1]
# * dp[0][0..n] = True
# The final result = dp[target][n]
dp = [[False for _ in xrange(n+1)] for _ in xrange(target+1)]
for i in xrange(n+1):
dp[0][i] = True
for s in xrange(1, target+1):
for i in xrange(1, n+1):
if s - numbers[i-1] < 0:
dp[s][i] = dp[s][i-1]
else:
dp[s][i] = dp[s][i-1] or dp[s - numbers[i-1]][i-1]
return dp[target][n]
As this question is not just asking whether such subset exists but return such subset, we can backtrack the dp array to figure out what decision we made in the past to get such result.
DP Solution with Backtracking: https://repl.it/@trsong/Subset-Sum
import unittest
def subset_sum_dp(numbers, target):
n = len(numbers)
dp = [[False for _ in xrange(n+1)] for _ in xrange(target+1)]
for i in xrange(n+1):
dp[0][i] = True
for s in xrange(1, target+1):
for i in xrange(1, n+1):
if s - numbers[i-1] < 0:
dp[s][i] = dp[s][i-1]
else:
dp[s][i] = dp[s][i-1] or dp[s - numbers[i-1]][i-1]
return dp[target][n], dp
def subset_sum(numbers, target):
if target == 0: return []
has_subset, dp = subset_sum_dp(numbers, target)
if not has_subset: return None
res = []
balance = target
for i in xrange(len(numbers), 0, -1):
delta = numbers[i-1]
if balance - delta >= 0 and dp[balance - delta][i-1]:
res.append(delta)
balance -= delta
return res
class SubsetSumSpec(unittest.TestCase):
def test_target_is_zero(self):
self.assertEqual(subset_sum([], 0), [])
self.assertEqual(subset_sum([1, 2], 0), [])
def test_subset_not_exist(self):
self.assertIsNone(subset_sum([], 1))
self.assertIsNone(subset_sum([2, 3], 1))
def test_more_than_one_subset(self):
res = sorted(subset_sum([3, 4, 2, 5], 7))
self.assertTrue(res == [3, 4] or res == [2, 5])
res2 = sorted(subset_sum([12, 1, 61, 5, 9, 2, 24], 24))
self.assertTrue(res2 == [1, 2, 9, 12] or res2 == [24])
if __name__ == '__main__':
unittest.main(exit=False)
May 27, 2019 [Medium] Multiset Partition
Question: Given a multiset of integers, return whether it can be partitioned into two subsets whose sums are the same.
For example, given the multiset {15, 5, 20, 10, 35, 15, 10}, it would return true, since we can split it up into {15, 5, 10, 15, 10} and {20, 35}, which both add up to 55.
Given the multiset {15, 5, 20, 10, 35}, it would return false, since we can’t split it up into two subsets that add up to the same sum.
Incorrect Solution:
def incorrect_solution(multiset):
# When input = [5, 1, 5, 1], expect result to be True but given False
if not multiset or len(multiset) <= 1: return False
sorted_multiset = sorted(multiset)
balance = 0
lo = 0
hi = len(multiset) - 1
while lo < hi:
if balance <= 0:
balance += sorted_multiset[lo]
lo += 1
else:
balance -= sorted_multiset[hi]
hi -= 1
return balance == 0
My thoughts: Initially I thought the problem is trivial as above, I simply sort the array and find a pivot position that can happen to break the array into two equal sum sub-arrays. However, I sooner realize that I cannot make assumption that one array will always have elements less than the other. eg. [4, 2, 1, 1] can break into [1, 2, 2] and [4] where all of 1, 2, 2 < 4. But [5, 1, 5, 1] does not work if break into [1, 1, 5] and [5].
Note: watch over for case
[5, 1, 5, 1]and[1, 2, 4, 3, 8]
After spend some time thinking more deeply about this issue, I find that this problem is actually equivalent to find target sum in subset. eg. Find subset in [5, 1, 5, 1] such that the sum equals 6.
Check out tomorrow’s question for subset sum.
DP Solution: https://repl.it/@trsong/Multiset-Partition
def has_equal_sum_partition(multiset):
if not multiset: return False
total = sum(multiset)
if total % 2 == 1: return False
target = total / 2
return subset_sum(multiset, target)
def subset_sum(numbers, target):
n = len(numbers)
# Let dp[sum][n] represent exiting subset of numbers[:n] with sum as sum:
# * dp[sum][n] = dp[sum][n-1] or dp[sum-a[n-1]][n-1]
# * dp[0][0..n] = True
# The final result = dp[target][n]
dp = [[False for _ in xrange(n+1)] for _ in xrange(target+1)]
for i in xrange(n+1):
dp[0][i] = True
for s in xrange(1, target+1):
for i in xrange(1, n+1):
if s - numbers[i-1] < 0:
dp[s][i] = dp[s][i-1]
else:
dp[s][i] = dp[s][i-1] or dp[s - numbers[i-1]][i-1]
return dp[target][n]
def main():
assert has_equal_sum_partition([5, 1, 5, 1])
assert not has_equal_sum_partition([1, 2, 2])
assert not has_equal_sum_partition([])
assert has_equal_sum_partition([15, 5, 20, 10, 35, 15, 10])
assert not has_equal_sum_partition([15, 5, 20, 10, 35])
assert has_equal_sum_partition([1, 2, 4, 3, 8])
if __name__ == '__main__':
main()
May 26, 2019 [Medium] Tic-Tac-Toe Game
Questions: Implementation of Tic-Tac-Toe game. Rules of the Game:
- The game is to be played between two people. One of the player chooses ‘O’ and the other ‘X’ to mark their respective cells.
- The game starts with one of the players and the game ends when one of the players has one whole row/ column/ diagonal filled with his/her respective character (‘O’ or ‘X’).
- If no one wins, then the game is said to be draw.
Follow-up: create a method that makes the next optimal move such that the person should never lose if make that move.
My thoughts: There are multiple ways to implement Tic-Tac-Toe. I choose to use Observer Pattern which can be used to solve all grid-like game.
From Wiki, Observer Pattern is used when there is one-to-many relationship between objects such as if one object is modified, its depenedent objects are to be notified automatically.
So basically, the way this pattern works is that each cell (the observable) has at most 4 observers: row obser, col observer, and two cross observers. Each observer is responsible for check if all cells underneth have the same value.
eg. If grid size is 3 and for cell at (1,1), row_observers contains all cells at row 1: (1,0), (1,1) and (1,2). col_observers has all cells at col 1: (1, 0), (1, 1) and (2, 1). Two cross observers check the diagonal cells (0, 0), (1, 1) and (2, 2) as well as (0, 2), (1, 1) and (2, 0). When we make a move at cell (1, 1), then all of 4 observers will be notified to check if all cell underneth have the same value, either ‘o’ or ‘x’. If there exists 1 observer satisfies, then the game ends. Otherwise, it continues.
Implementation Using Observer Pattern: https://repl.it/@trsong/Tic-Tac-Toe-Game
class CellObserver(object):
def __init__(self, cell, neighbors):
self._cell = cell
self._neighbors = neighbors
def notify(self):
return all(neighbor.val == self._cell.val for neighbor in self._neighbors)
class CellSubject(object):
def __init__(self, val='_'):
self.val = val
self._observers = []
def add_observer(self, cell_observer):
self._observers.append(cell_observer)
def notify_observers(self):
return any(observer.notify() for observer in self._observers)
class Grid(object):
def __init__(self, size, first_player='x'):
self._next_move = first_player
self._size = size
self._reset()
def _reset(self):
n = self._size
self._turn = 0
self._game_finished = False
self._table = [[ CellSubject() for _ in xrange(n)] for _ in xrange(n)]
row_neighbors = [None] * n
col_neighbors = [None] * n
for i in xrange(n):
row_neighbors[i] = [self._table[i][col] for col in xrange(n)]
col_neighbors[i] = [self._table[row][i] for row in xrange(n)]
for i in xrange(n):
for j in xrange(n):
cell = self._table[i][j]
cell.add_observer(CellObserver(cell, row_neighbors[i]))
cell.add_observer(CellObserver(cell, col_neighbors[j]))
top_left_to_bottom_right = [self._table[i][i] for i in xrange(n)]
for i in xrange(n):
cell = self._table[i][i]
cell.add_observer(CellObserver(cell, top_left_to_bottom_right))
top_right_to_bottom_left = [self._table[i][n-1-i] for i in xrange(n)]
for i in xrange(n):
cell = self._table[i][n-1-i]
cell.add_observer(CellObserver(cell, top_right_to_bottom_left))
def _switch_player(self):
self._next_move = 'o' if self._next_move == 'x' else 'x'
def get_next_move(self):
return self._next_move
def display(self):
for row in xrange(self._size):
print ','.join(cell.val for cell in self._table[row])
def move(self, row, col):
if not (0 <= row < self._size and 0 <= col < self._size):
print "row or col out of range."
return
cell = self._table[row][col]
if cell.val != '_':
print "Cell has been occupied. Choose a different cell"
else:
self._turn += 1
cell.val = self._next_move
self._game_finished = cell.notify_observers()
self._switch_player()
def is_game_finished(self):
return self._game_finished or self._turn > self._size * self._size
def result(self):
if self._turn <= self._size * self._size and self._game_finished:
loser = self.get_next_move()
winner = 'o' if loser == 'x' else 'x'
return 'Game over. %s wins.' % winner
else:
return "No one wins. There is a tie"
class Game(object):
def start(self):
print '====== Welcome to Tic-Tac-Toe Game ======'
while not raw_input("Press Enter to start..."):
self.game_init()
def game_init(self):
size = int(input('Please choose grid size: '))
self._grid = Grid(size)
while not self._grid.is_game_finished():
r, c = [int(x) for x in raw_input("Next player place %s in row, col: " % self._grid.get_next_move()).split(',')]
self._grid.move(r, c)
self._grid.display()
print self._grid.result()
def test(self):
self._grid = Grid(3)
self._grid.move(0, 0)
self._grid.move(1, 1)
self._grid.move(2, 2)
self._grid.move(0, 1)
self._grid.move(2, 1)
self._grid.move(2, 0)
self._grid.move(0, 2)
self._grid.move(1, 2)
self._grid.move(1, 0)
assert self._grid.result() == "No one wins. There is a tie"
self._grid = Grid(1)
self._grid.move(0, 0)
assert self._grid.result() == "Game over. x wins."
class main():
game = Game()
game.test()
game.start()
if __name__ == '__main__':
main()
Game demo
====== Welcome to Tic-Tac-Toe Game ======
Press Enter to start...
Please choose grid size: 3
Next player place x in row, col: 1,1
_,_,_
_,x,_
_,_,_
Next player place o in row, col: 0,1
_,o,_
_,x,_
_,_,_
Next player place x in row, col: 0,0
x,o,_
_,x,_
_,_,_
Next player place o in row, col: 2,2
x,o,_
_,x,_
_,_,o
Next player place x in row, col: 3,0
row or col out of range.
x,o,_
_,x,_
_,_,o
Next player place x in row, col: 0,0
Cell has been occupied. Choose a different cell
x,o,_
_,x,_
_,_,o
Next player place x in row, col: 2,0
x,o,_
_,x,_
x,_,o
Next player place o in row, col: 0,2
x,o,o
_,x,_
x,_,o
Next player place x in row, col: 1,0
x,o,o
x,x,_
x,_,o
Game over. x wins.
Press Enter to start...
Follow-up Question. TODO tsong: It’s 3:30 am, and I’m just too tired. I was planning to implement that using Backtracking algorithem. However, my mind is kinda dizzy and it’s time to get some rest. I will probably go back to this question once get a chance in the future.
May 25, 2019 [Easy] Run-length Encoding
Question: Run-length encoding is a fast and simple method of encoding strings. The basic idea is to represent repeated successive characters as a single count and character. For example, the string “AAAABBBCCDAA” would be encoded as “4A3B2C1D2A”.
Implement run-length encoding and decoding. You can assume the string to be encoded have no digits and consists solely of alphabetic characters. You can assume the string to be decoded is valid.
Python Solution: https://repl.it/@trsong/Run-length-Encoding
class Run_Length_Encoding(object):
@staticmethod
def decode(text):
if not text: return ""
i = 0
res = []
while i < len(text):
repeat = 0
while '0' <= text[i] <= '9':
repeat = 10 * repeat + int(text[i])
i += 1
res.append(text[i] * repeat)
i += 1
return ''.join(res)
@staticmethod
def encode(text):
if not text: return ""
i = 0
res = []
while i < len(text):
cur = text[i]
repeat = 1
i += 1
while i < len(text) and text[i] == cur:
repeat += 1
i += 1
res.append("{}{}".format(repeat, cur))
return ''.join(res)
def test_result(raw_text, encoded_text):
assert Run_Length_Encoding.encode(raw_text) == encoded_text
assert Run_Length_Encoding.decode(encoded_text) == raw_text
def main():
test_result("", "")
test_result("ABC", "1A1B1C")
test_result("A"*10, "10A")
test_result("A" * 100 + "B" + "C" * 99, "100A1B99C")
test_result("ABBCCCDDDDCCCBBA", "1A2B3C4D3C2B1A")
if __name__ == '__main__':
main()
May 24, 2019 [Medium] Maximum Subarray Sum
Question: Given an array of numbers, find the maximum sum of any contiguous subarray of the array.
For example, given the array [34, -50, 42, 14, -5, 86], the maximum sum would be 137, since we would take elements 42, 14, -5, and 86.
Given the array [-5, -1, -8, -9], the maximum sum would be 0, since we would not take any elements.
Do this in O(N) time.
My thoughts: Start from trival examples and then generalize our solution.
Properties can be derived from trivial example:
- if all nums are positive, then the result equals sum of all of them
- if all nums are negative, then the result equals 0.
Consider we have answer when the input size equals i - 1. Then when we encouter the ith element:
- if it’s positive, then we use property 1
- if it’s negative, but when include the current num, the result is still positive, then we still use property 1. ‘coz the list is equivalent to some all positive list.
- if it’s negative, but even we include the current, the result is negative, then we use property 2. ‘coz the list is equivalent to some all negative list.
Python Solution: https://repl.it/@trsong/Maximum-Subarray-Sum
def max_sub_array(nums):
if not nums: return 0
max_sum = 0
accu_sum = 0
for num in nums:
if num > 0:
accu_sum += num
max_sum = max(max_sum, accu_sum)
elif accu_sum + num > 0:
accu_sum += num
else:
# when accu_sum + num <= 0
accu_sum = 0
return max_sum
def main():
assert max_sub_array([]) == 0
assert max_sub_array([1]) == 1
assert max_sub_array([-1]) == 0
assert max_sub_array([34, -50, 42, 14, -5, 86]) == 137
assert max_sub_array([-5, -1, -8, -9]) == 0
assert max_sub_array([-1, -1, -1, 5, -1 , -1]) == 5
assert max_sub_array([1, 1, -5, 1, 1]) == 2
assert max_sub_array([1, 1, -1, 1, 1]) == 3
assert max_sub_array([1, 1, -1, 1, 1, 1]) == 4
if __name__ == '__main__':
main()
May 23, 2019 [Hard] LRU Cache
Question: Implement an LRU (Least Recently Used) cache. It should be able to be initialized with a cache size n, and contain the following methods:
set(key, value): sets key to value. If there are already n items in the cache and we are adding a new item, then it should also remove the least recently used item.
get(key): gets the value at key. If no such key exists, return null.Each operation should run in O(1) time.
My thoughts: The implementation of LRU cache can be similar to Linked Hash Map: a map that also preserve the insertion order. It has a lookup table for fast value retrival and a doubly linked list to keep track of least recent used item that can be evicted when the cache is full.
However, during interview, usually the candidate will be asked to use a singly linked list to implement (once during SAP on-site). The trick is to figure out a way to remove an element in a singly linked list which can be achived use the following:
node.val = node.next.val
node.next = node.next.next
Note that above method not work if attempt to remove the very last element which will cause null pointer exception. A way to overcome this issue is to create a dummy node at the end of list.
P.S: For doubly linked list solution check LC 146.
Singly Linked-List Solution: https://repl.it/@trsong/LRU-Cache
class ListNode(object):
def __init__(self, key=None, val=None, next=None):
self.key = key
self.val = val
self.next = next
class LRUCache(object):
def __init__(self, capacity):
self._capacity = capacity
self._size = 0
self._start = ListNode()
self._end = self._start
self._lookup = {}
def _populate(self, key):
node = self._lookup[key]
# Duplicate node and append it to the end of list
self._end.key, self._end.val, self._end.next = node.key, node.val, ListNode()
self._lookup[node.key] = self._end
self._end = self._end.next
# Remove node
node.key, node.val, node.next = node.next.key, node.next.val, node.next.next
self._lookup[node.key] = node
def get(self, key):
if key not in self._lookup: return None
self._populate(key)
return self._lookup[key].val
def set(self, key, val):
if key in self._lookup:
self._lookup[key].val = val
self._populate(key)
else:
if self._size >= self._capacity:
del self._lookup[self._start.key]
self._start = self._start.next
self._size -= 1
self._start = ListNode(key, val, self._start)
self._lookup[key] = self._start
self._populate(key)
self._size += 1
def main():
cache = LRUCache(3)
cache.set(0, 0) # Least Recent -> 0 -> Most Recent
cache.set(1, 1) # Least Recent -> 0, 1 -> Most Recent
cache.set(2, 2) # Least Recent -> 0, 1, 2 -> Most Recent
cache.set(3, 3) # Least Recent -> 1, 2, 3 -> Most Recent. Evict 0
assert cache.get(0) is None
assert cache.get(2) == 2 # Least Recent -> 1, 3, 2 -> Most Recent
cache.set(4, 4) # Least Recent -> 3, 2, 4 -> Most Recent. Evict 1
assert cache.get(1) is None
assert cache.get(2) == 2 # Least Recent -> 3, 4, 2 -> Most Recent
assert cache.get(3) == 3 # Least Recent -> 4, 2, 3 -> Most Recent
assert cache.get(2) == 2 # Least Recent -> 4, 3, 2 -> Most Recent
cache.set(5, 5) # Least Recent -> 3, 2, 5 -> Most Recent. Evict 4
cache.set(6, 6) # Least Recent -> 2, 5, 6 -> Most Recent. Evict 3
assert cache.get(4) is None
assert cache.get(3) is None
cache.set(7, 7) # Least Recent -> 5, 6, 7 -> Most Recent. Evict 2
assert cache.get(2) is None
if __name__ == '__main__':
main()
May 22, 2019 [Easy] Special Stack
Question: Implement a special stack that has the following methods:
push(val), which pushes an element onto the stackpop(), which pops off and returns the topmost element of the stack. If there are no elements in the stack, then it should throw an error or return null.max(), which returns the maximum value in the stack currently. If there are no elements in the stack, then it should throw an error or return null.Each method should run in constant time.
Python Solution: https://repl.it/@trsong/Special-Stack
class ListNode(object):
def __init__(self, val, next=None):
self.val = val
self.next = next
class SpecialStack(object):
def __init__(self):
self._stack = None
self._max_stack = None
self._size = 0
def push(self, val):
max_val = max(val, self._max_stack.val) if self._size > 0 else val
self._max_stack = ListNode(max_val, self._max_stack)
self._stack = ListNode(val, self._stack)
self._size += 1
def pop(self):
if self._size <= 0:
return None
else:
val = self._stack.val
self._stack = self._stack.next
self._max_stack = self._max_stack.next
self._size -= 1
return val
def max(self):
if self._size <= 0:
return None
else:
return self._max_stack.val
def main():
stack = SpecialStack()
assert stack.pop() is None
assert stack.max() is None
stack.push(1)
stack.push(2)
stack.push(3)
assert stack.max() == 3
assert stack.pop() == 3
assert stack.max() == 2
assert stack.pop() == 2
assert stack.pop() == 1
assert stack.pop() is None
stack.push(3)
stack.push(2)
stack.push(1)
assert stack.max() == 3
assert stack.pop() == 1
assert stack.pop() == 2
if __name__ == '__main__':
main()
May 21, 2019 [Hard] Random Elements from Infinite Stream (Reservoir Sampling)
Question: Randomly choosing a sample of k items from a list S containing n items, where n is either a very large or unknown number. Typically, n is too large to fit the whole list into main memory.
My thoughts: Choose k elems randomly from an infitite stream can be tricky. We should simplify this question, find the pattern and then generalize the solution. So, let’s first think about how to randomly get one element from the stream:
As the input stream can be arbitrarily large, our solution must be able to calculate the chosen element on the fly. So here comes the strategy:
When consume the i-th element:
- Either choose the i-th element with 1/(i+1) chance.
- Or, keep the last chosen element with 1 - 1/(i+1) chance.
Above is also called Reservoir Sampling.
Proof by Induction:
- Base case: when there is 1 element, then the 0th element is chosen by
1/(0+1) = 100%chance. - Inductive Hypothesis: Suppose for above strategy works for all elemements between 0th and i-1th, which means all elem has
1/ichance to be chosen. - Inductive Step: when consume the i-th element:
- If the i-th element is selected with
1/(i+1)chance, then it works for the i-th element - As for other elements to be choosen, we will have
1-1/(i+1)chance not to choose the i-th element. And also based on the Inductive Hypothesis: all elemements between 0th and i-1th has 1/i chance to be chosen. Thus, the chance of any elem between 0-th to i-th element to be chosen in this round eqauls1/i * (1-(1/(i+1))) = 1/(i+1), which means you cannot choose the i-th element and at the same time you choose any element between 0-th and i-th element. Therefore it works for all previous elements as each element has1/(i+1)chance to be chosen.
- If the i-th element is selected with
Random One Element Solution: https://repl.it/@trsong/Random-One-Elem
from random import randint
def random_one_elem(stream):
pick = None
for i, elem in enumerate(stream):
if i == 0 or randint(0, i) == 0:
# Has 1/(i+1) chance to pick i-th elem
pick = elem
return pick
def print_distribution(stream, repeat):
histogram = {}
for _ in xrange(repeat):
res = random_one_elem(stream)
if res not in histogram:
histogram[res] = 0
histogram[res] += 1
print histogram
def main():
# Distribution looks like {0: 1003, 1: 1004, 2: 943, 3: 994, 4: 1023, 5: 1019, 6: 1013, 7: 1025, 8: 1005, 9: 971}
print_distribution(xrange(10), repeat=10000)
if __name__ == '__main__':
main()
Ever since for randomly choose 1 element, we keep 1 chosen element during execution, k elements will be kept and we will use the following strategy to keep and kick out elements:
When consume the i-th element:
- Either choose the i-th element with k/(i+1) chance. (And kick out any of the chosen k element)
- Or, keep the last chosen elements with 1 - k/(i+1) chance.
Similar to previous proof to show that each element has 1/(i+1) chance. It can be easily shown that each element has k/(i+1) to be chosen. Just google Reservoir Sampling if you are curious about other strategies.
Random K Elements Solution: https://repl.it/@trsong/Random-K-Elem
from random import randint
def random_k_elem(stream, k):
pick = [None] * k
for i, elem in enumerate(stream):
if i < k:
pick[i] = elem
elif randint(1, i+1) <= k:
# The i-th elem has k/(n+1) chance to be picked
pick[randint(0, k-1)] = elem
return pick
def print_distribution(stream, k, repeat):
histogram = {}
for _ in xrange(repeat):
res = random_k_elem(stream, k)
for e in res:
if e not in histogram:
histogram[e] = 0
histogram[e] += 1
print histogram
def main():
# Distribution looks like:
# {0: 2984, 1: 3008, 2: 3085, 3: 3045, 4: 3075, 5: 3001, 6: 2923, 7: 2913, 8: 2954, 9: 3012}
print_distribution(xrange(10), k=3, repeat=10000)
if __name__ == '__main__':
main()
May 20, 2019 [Hard] Edit Distance
Question: The edit distance between two strings refers to the minimum number of character insertions, deletions, and substitutions required to change one string to the other. For example, the edit distance between “kitten” and “sitting” is three: substitute the “k” for “s”, substitute the “e” for “i”, and append a “g”.
Given two strings, compute the edit distance between them.
A little bit background information: I first learnt this question in my 3rd year algorithem class. At that moment, this question was introduced to illustrate how dynamic programming works. And even nowadays, I can still recall the formula to be something like dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + (0 if source[i] == target[j] else 1). However, when I ask my friends what dp represents in this question and how above formula works, few can give me convincing explanation. So the same thing could happen to readers like you: if you just know the formula without understanding which part represents insertion, removal or updating, then probably you just memorize the solution and pretend you understand the answer. And what could happen in the near future is that the next time when a similar question, like May 19 Regular expression, shows up during interview, you end up spending 20 min, got stuck trying to come up w/ dp formula.
My thoughts: My suggestion is that let’s forget about dp at first, and we should just focus on recursion. (The idea between those two is kinda the same.) Just use the following template you learnt in first year of university to figure out the solution:
def recursion(input):
if ...base case...:
return ...base case solution...
else:
do something to first of input
return recursion(rest of input)
def recursion2(input1, input2):
if ...base case...:
return ...base case solution...
else:
do something to first of input1
do something to first of input2
res1 = recursion2(rest of input1, input2)
res2 = recursion2(input1, rest of input2)
res3 = recursion2(rest of input1, rest of input2)
return do something to res1, res2, res3
def recursion3(input1, input2):
if ...base case...:
return ...base case solution...
else:
do something to last of input1
do something to last of input2
res1 = recursion3(drop last of input1, input2)
res2 = recursion3(input1, drop last of input2)
res3 = recursion3(drop last of input1, drop last of input2)
return do something to res1, res2, res3
Since we have two inputs for this question, we can either use recursion2 or recursion3 in above template, it doesn’t really matter in this question. def edit_distance(source, target). And now let’s think about what is the base case. Base case is usually something trivial, like empty list. Then it’s easy to know that if either source or target is empty, the edit distance is the other one’s length. e.g. edit_distance("", "kitten") == 6
Then let’s think about how we can shrink the size of source and target. In above template, there are 3 different ways to shrink the input size. Check the line res1, res2 and res3.
-
Shrink source size:
I came up w/ some example like
edit_distance("ab", "a")andedit_distance("a", "a"). Now think about the relationship between them. It turns outedit_distance("ab", "a") == 1 + edit_distance("a", "a"). As the minimum edit we need is just remove “b” from “ab” in source: only 1 extra edit. -
Shrink target size:
I came up w/ some example like
edit_distance("a", "ab")andedit_distance("a", "a"). It turns out the mimum edit is to append “b” to the source “a” that gives “ab”. Soedit_distance("a", "ab") == 1 + edit_distance("a", "a"). -
Shrink both source and target size:
I came up w/ some example like
edit_distance("aa", "ab")andedit_distance("a", "a"). It seems we just need to replace “a” with “b” or “b” with “a”. So only 1 more edit should be sufficient. However if we haveedit_distance("ab", "ab")andedit_distance("a", "a"). Then that means we don’t need to do anything when there is a match. That givesedit_distance("aa", "ab") = 1 + edit_distance("a", "a")andedit_distance("ab", "ab") == edit_distance("a", "a")
Note that any of res1, res2 and res3 might give the mimum edit. So we need to apply min to get the smallest among them.
Python Solution: https://repl.it/@trsong/Edit-Distance
def edit_distance(source, target):
if not source or not target:
return max(len(source), len(target))
# The edit_distance when insert/append an elem to source to match last elem in target
insert_res = edit_distance(source, target[:-1]) + 1
# The edit_distance when update last elem in source to match last elem in target
update_res = edit_distance(source[:-1], target[:-1]) + (0 if source[-1] == target[-1] else 1)
# The edit_distance when remove the last elem from source
remove_res = edit_distance(source[:-1], target) + 1
return min(insert_res, update_res, remove_res)
# If we modify the algorithem to insert/update/remove upon the first elem, it also works
def edit_distance2(source, target):
if not source or not target:
return max(len(source), len(target))
# The edit_distance when insert/prepend an elem to source to match the first elem in target
insert_res = edit_distance2(source, target[1:]) + 1
# The edit_distance when update the first elem in source to match the first elem in target
update_res = edit_distance2(source[1:], target[1:]) + (0 if source[0] == target[0] else 1)
# The edit_distance when remove the first elem from source
remove_res = edit_distance2(source[1:], target) + 1
return min(insert_res, update_res, remove_res)
def main():
assert edit_distance("kitten", "sitting") == 3
assert edit_distance("sitting", "kitten") == 3
assert edit_distance("sitting", "") == 7
assert edit_distance("", "kitten") == 6
assert edit_distance("", "") == 0
if __name__ == "__main__":
main()
Note: Above solution can be optimized using a cache. Or based on recursive formula, generate DP array. However, I feel too lazy for DP solution, you can probably google Levenshtein Distance or “edit distance”. Here, I just give the optimized solution w/ cache. You can see how similar the dp solution vs optimziation w/ cache. And the benefit of using cache is that, you don’t need to figure out the order to fill dp array as well as the initial value for dp array which is quite helpful. If you are curious about what question can give a weird dp filling order, just check May 19 question: Regular Expression and try to solve that w/ dp.
Python Solution w/ Cache: https://repl.it/@trsong/Edit-Distance-with-Cache
def edit_distance_helper(source, target, i, j, cache):
# The edit_distance when insert/prepend an elem to source to match the first elem in target
insert_res = edit_distance_helper_with_cache(source, target, i, j + 1, cache) + 1
# The edit_distance when update the first elem in source to match the first elem in target
update_res = edit_distance_helper_with_cache(source, target, i + 1, j + 1, cache) + (0 if source[i] == target[j] else 1)
# The edit_distance when remove the first elem from source
remove_res = edit_distance_helper_with_cache(source, target, i + 1, j, cache) + 1
return min(insert_res, update_res, remove_res)
# edit_distance(source[i:], target[j:])
def edit_distance_helper_with_cache(source, target, i, j, cache):
n, m = len(source), len(target)
if i > n - 1 or j > m - 1:
return max(n - i, m - j)
if cache[i][j] is None:
cache[i][j] = edit_distance_helper(source, target, i, j, cache)
return cache[i][j]
def edit_distance(source, target):
n, m = len(source), len(target)
cache = [[None for _ in range(m)] for _ in range(n)]
return edit_distance_helper_with_cache(source, target, 0, 0, cache)
May 19, 2019 [Hard] Regular Expression: Period and Asterisk
Question: Implement regular expression matching with the following special characters:
.(period) which matches any single character
*(asterisk) which matches zero or more of the preceding elementThat is, implement a function that takes in a string and a valid regular expression and returns whether or not the string matches the regular expression.
For example, given the regular expression “ra.” and the string “ray”, your function should return true. The same regular expression on the string “raymond” should return false.
Given the regular expression “.*at” and the string “chat”, your function should return true. The same regular expression on the string “chats” should return false.
My thoughts: First consider the solution without * (asterisk), then we just need to match letters one by one while doing some special handling for . (period) so that it can match all letters.
Then we consider the solution with *, we will need to perform ONE look-ahead, so * can represent 0 or more matching. And we consider those two situations separately:
- If we have 1 matching, we just need to check if the rest of text match the current pattern.
- Or if we do not have matching, then we need to advance both text and pattern.
Python Solution: https://repl.it/@trsong/Pattern-Match
def pattern_match(text, pattern):
if not pattern: return not text
match_first = text and (text[0] == pattern[0] or pattern[0] == '.')
if len(pattern) > 1 and pattern[1] == '*':
# Either match first letter and continue check on rest; Or not match at all
return match_first and pattern_match(text[1:], pattern) or pattern_match(text, pattern[2:])
else:
# Without "*", we will proceed both text and pattern
return match_first and pattern_match(text[1:], pattern[1:])
def main():
assert not pattern_match("a", "")
assert not pattern_match("", "a")
assert pattern_match("", "")
assert pattern_match("aa", "a*")
assert pattern_match("aaa", "ab*ac*a")
assert pattern_match("aab", "c*a*b")
assert pattern_match("ray", "ra.")
assert not pattern_match("raymond", "ra.")
assert pattern_match("chat", ".*at")
assert not pattern_match("chats", ".*at")
if __name__ == '__main__':
main()
Notice that as we keep calling
text[1:],pattern[1:]andpattern[2:]in recursive calls, there are certain results that can be cached so that none of the same input will be executed twice. Also, keep generating substring is expensive, we should replace it w/ in-place checking by passing index.
Python Solution with Cache: https://repl.it/@trsong/Pattern-Match2
def pattern_match_helper(text, pattern, i, j, cache):
n, m = len(text), len(pattern)
match_first = i < n and (text[i] == pattern[j] or pattern[j] == '.')
if j < m - 1 and pattern[j+1] == '*':
# Either match first letter and continue check on rest; Or not match at all
return match_first and pattern_match_helper_with_cache(text, pattern, i+1, j, cache) or pattern_match_helper_with_cache(text, pattern, i, j+2, cache)
else:
# Without "*", we will proceed both text and pattern
return match_first and pattern_match_helper_with_cache(text, pattern, i+1, j+1, cache)
def pattern_match_helper_with_cache(text, pattern, i, j, cache):
n, m = len(text), len(pattern)
if j >= m: return i >= n
if cache[i][j] is None:
cache[i][j] = pattern_match_helper(text, pattern, i, j, cache)
return cache[i][j]
def pattern_match(text, pattern):
if not pattern: return not text
cache = [[None for _ in xrange(len(pattern)+1)] for _ in xrange(len(text)+1)]
return pattern_match_helper(text, pattern, 0, 0, cache)
May 18, 2019 [Easy] Intersecting Node
Question: Given two singly linked lists that intersect at some point, find the intersecting node. The lists are non-cyclical.
For example, given A = 3 -> 7 -> 8 -> 10 and B = 99 -> 1 -> 8 -> 10, return the node with value 8.
In this example, assume nodes with the same value are the exact same node objects.
Do this in O(M + N) time (where M and N are the lengths of the lists) and constant space.
My thoughts: For two lists w/ same length, say [1, 2, 3] and [4, 2, 3], the intersecting node is the first element shared by two list when iterate through both lists at the same time. In above example, 2 is the elem we are looking for.
For two lists w/ different length, say [1, 1, 1, 2 3] and [4, 2, 3]. We can convert this case into above case by first calculating the length difference between those two lists and let larger list proceed that difference number of nodes ahead of time. Then we will end up w/ 2 lists of the same length.
eg. The difference between [1, 1, 1, 2 3] and [4, 2, 3] is 2. We proceed the pointer of larger list by 2, gives [1, 2, 3]. Thus we have 2 lists of the same length.
Python Soluion: https://repl.it/@trsong/Intersecting-Node
class ListNode(object):
def __init__(self, val, next=None):
self.val = val
self.next = next
def get_intersecting_node(lst1, lst2):
l1, l2 = lst1, lst2
len1, len2 = 0, 0
while l1:
l1 = l1.next
len1 += 1
while l2:
l2 = l2.next
len2 += 1
long_list, short_list = lst1, lst2
diff = len1 - len2
if diff < 0:
long_list, short_list = lst2, lst1
diff = -diff
for _ in xrange(diff):
long_list = long_list.next
while long_list != short_list:
long_list = long_list.next
short_list = short_list.next
return long_list
def main():
shared = ListNode(8, ListNode(0))
l1 = ListNode(3, ListNode(7, shared))
l2 = ListNode(99, ListNode(1, shared))
assert get_intersecting_node(l1, l2).val == 8
assert get_intersecting_node(l2, l1).val == 8
l3 = ListNode(10, ListNode(11, l1))
assert get_intersecting_node(l3, l2).val == 8
assert get_intersecting_node(l2, l3).val == 8
assert get_intersecting_node(None, None) is None
assert get_intersecting_node(l1, None) is None
assert get_intersecting_node(None, l1) is None
if __name__ == '__main__':
main()
May 17, 2019 LC 332 [Medium] Reconstruct Itinerary
Questions: Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.
Note:
- If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary [“JFK”, “LGA”] has a smaller lexical order than [“JFK”, “LGB”].
- All airports are represented by three capital letters (IATA code).
- You may assume all tickets form at least one valid itinerary.
Example 1:
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]
Example 2:
Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
But it is larger in lexical order.
My thoughts: Forget about lexical requirement for now, consider all airports as vertices and each itinerary as an edge. Then all we need to do is to find a path from “JFK” that consumes all edges. By using DFS to iterate all potential solution space, once we find a solution we will return immediately.
Now let’s consider the lexical requirement, when we search from one node to its neighbor, we can go from smaller lexical order first and by keep doing that will lead us to the result.
Python Solution: https://repl.it/@trsong/Reconstruct-Itinerary
def search_itinerary_DFS(src, itinerary_lookup, route_res):
# Using DFS to find a solution that can consume all edges
while src in itinerary_lookup and itinerary_lookup[src]:
search_itinerary_DFS(itinerary_lookup[src].pop(0), itinerary_lookup, route_res)
# Once find a route, build the routes in reverse order so that source will go before destination
route_res.insert(0, src)
def reconstruct_itinerary(tickets):
itinerary_lookup = {}
# Build up neighbor lookup table
for it in tickets:
src, dst = it
if src not in itinerary_lookup:
itinerary_lookup[src] = [dst]
else:
itinerary_lookup[src].append(dst)
# Sort all destinations in alphabet order so that smaller lexical order comes first
for key in itinerary_lookup.keys():
itinerary_lookup[key] = sorted(itinerary_lookup[key])
res = []
search_itinerary_DFS("JFK", itinerary_lookup, res)
return res
def main():
assert reconstruct_Itinerary([["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]) == ["JFK", "MUC", "LHR", "SFO", "SJC"]
assert reconstruct_Itinerary([["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]) == ["JFK","ATL","JFK","SFO","ATL","SFO"]
assert reconstruct_Itinerary([["JFK", "YVR"], ["LAX", "LAX"], ["YVR", "YVR"], ["YVR", "YVR"], ["YVR", "LAX"], ["LAX", "LAX"], ["LAX", "YVR"], ["YVR", "JFK"]]) == ['JFK', 'YVR', 'LAX', 'LAX', 'LAX', 'YVR', 'YVR', 'YVR', 'JFK']
if __name__ == '__main__':
main()
May 16, 2019 [Easy] Minimum Lecture Rooms
Questions: Given an array of time intervals (start, end) for classroom lectures (possibly overlapping), find the minimum number of rooms required.
For example, given [(30, 75), (0, 50), (60, 150)], you should return 2.
My thoughts: In order to solve this problem, do NOT worry about minimum at first. Think about how many rooms we might need by testing different examples:
Exreme Case
- If there are 10 intervals that all of them are overlapping w/ each other, then we need 10 rooms at peak hours
- If there are 10 intervals that none of them are overlapping w/ each other, then 1 room is sufficient to hold all 10 intervals one by one
Normal Case
- If we just have 1 interval, if we need 1 room
- If we have 2 intervals that might overlapping at some point, then we need to add 1 more room, which gives 2 in total. eg. (1, 10) and (5, 15)
- If we have 3 intervals that
- all of them overlapping at some point, then we need to add 2 more rooms, which gives 3 in total eg. (1, 10), (5, 15) and (6, 15)
- 2 of them overlapping at some point, then we only ned to add 1 more rooms, which gives 2 in total eg. (1, 10), (5, 15) and (10, 15)
For (1, 10), (5, 15) and (6, 15) we can use the folling time table to find the pattern
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| total room at t | 0 | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 0 | 0 |
| difference | 0 | +1 | 0 | 0 | 0 | +1 | +1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | -2 | 0 |
Note: Did you notice whenever we enter an interval at time t, the total number of room at time t
+1and whenever we leave an interval the total number-1? e.g.+1att = 1, 5, 6and-1att=10, 15, 15. And at peak hour, the total room equals 3.
Counting Sort Python Solution: https://repl.it/@trsong/Minimum-Lecture-Rooms
def min_lec_room(intervals):
min_start = 0
max_end = 0
for elem in intervals:
min_start = min(min_start, elem[0])
max_end = max(max_end, elem[1])
# To save space, we only start time at min_start instead of time = 0
room_at = [0] * (max_end - min_start + 1)
for elem in intervals:
room_at[elem[0] - min_start] += 1
room_at[elem[1] - min_start] -= 1
max_accumulated_room = 0
accumulated_room = 0
for t in range(max_end - min_start + 1):
accumulated_room += room_at[t]
max_accumulated_room = max(max_accumulated_room, accumulated_room)
return max_accumulated_room
def main():
t1 = (-10, 0)
t2 = (-5, 5)
t3 = (0, 10)
t4 = (5, 15)
assert min_lec_room([t1, t1, t1]) == 3
assert min_lec_room([(30, 75), (0, 50), (60, 150)]) == 2
assert min_lec_room([t3, t1]) == 1
assert min_lec_room([t1, t3, t2, t4]) == 2
assert min_lec_room([t4, t3, t2, t1, t1, t2, t3, t4]) == 4
if __name__ == '__main__':
main()
Note: in order to save space, can we just calculate at either start time or end time?
For (1, 10), (5, 15) and (6, 15), in order to save space, we just consider end point
| t | 1 | 5 | 6 | 10 | 15 |
|---|---|---|---|---|---|
| total room at t | 1 | 2 | 3 | 2 | 0 |
| difference | +1 | +1 | +1 | -1 | -2 |
Python Solution: https://repl.it/@trsong/Minimum-Lecture-Rooms2
def min_lec_room(intervals):
begins = [(e[0], 1) for e in intervals]
ends = [(e[1], -1) for e in intervals]
all_points = begins + ends
sorted_all_points = sorted(all_points, key=lambda x: x[0])
max_accumulated_room = 0
accumulated_room = 0
i = 0
while i < len(sorted_all_points):
accu = sorted_all_points[i][1]
# Combine all the rooms for the same time
while i + 1 < len(sorted_all_points) and sorted_all_points[i+1][0] == sorted_all_points[i][0]:
accu += sorted_all_points[i+1][1]
i += 1
accumulated_room += accu
max_accumulated_room = max(max_accumulated_room, accumulated_room)
i += 1
return max_accumulated_room
def main():
t1 = (-10, 0)
t2 = (-5, 5)
t3 = (0, 10)
t4 = (5, 15)
assert min_lec_room([t1, t1, t1]) == 3
assert min_lec_room([(30, 75), (0, 50), (60, 150)]) == 2
assert min_lec_room([t3, t1]) == 1
assert min_lec_room([t1, t3, t2, t4]) == 2
assert min_lec_room([t4, t3, t2, t1, t1, t2, t3, t4]) == 4
if __name__ == '__main__':
main()
May 15, 2019 [Medium] Tokenization
Questions: Given a dictionary of words and a string made up of those words (no spaces), return the original sentence in a list. If there is more than one possible reconstruction, return any of them. If there is no possible reconstruction, then return null.
For example, given the set of words ‘quick’, ‘brown’, ‘the’, ‘fox’, and the string “thequickbrownfox”, you should return [‘the’, ‘quick’, ‘brown’, ‘fox’].
Given the set of words [‘bed’, ‘bath’, ‘bedbath’, ‘and’, ‘beyond’], and the string “bedbathandbeyond”, return either [‘bed’, ‘bath’, ‘and’, ‘beyond] or [‘bedbath’, ‘and’, ‘beyond’].
My thoughts: Divide and Conquer Break the word into smaller chunks: prefix and suffix. Process either of them and doing recursion on the other one.
Suppose process(word) = [word] if word in dictionary
Then tokenization("thequickbrownfox") = Any of the following result
tokenization("thequickbrownfox") + process("") => None
tokenization("thequickbrownfo") + process("x") => None
tokenization("thequickbrownf") + process("ox") => None
tokenization("thequickbrown") + process("fox") => tokenization("thequickbrown") + ["fox"]
tokenization("thequickbrow") + process("nfox") => None
tokenization("thequickbro") + process("wnfox") => None
tokenization("thequickbr") + process("ownfox") => None
tokenization("thequickb") + process("rownfox") => None
tokenization("thequick") + process("brownfox") => None
tokenization("thequic") + process("kbrownfox") => None
tokenization("thequ") + process("ickbrownfox") => None
tokenization("theq") + process("uickbrownfox") => None
tokenization("the") + process("quickbrownfox") => None
tokenization("th") + process("equickbrownfox") => None
tokenization("t") + process("hequickbrownfox") => None
tokenization("") + process("thequickbrownfox") => None
Python Solution: https://repl.it/@trsong/Tokenization
def tokenization_recur(word, dictionary):
if not word:
return []
for i in xrange(len(word)):
suffix = word[i:]
processed_suffix = [suffix] if not suffix or suffix in dictionary else None
if not processed_suffix: continue
processed_prefix = tokenization_recur(word[:i], dictionary)
if processed_prefix is not None:
return processed_prefix + processed_suffix
return None
def tokenization(word, dictionary):
if not word or not dictionary:
return None
else:
res = tokenization_recur(word, set(dictionary))
return ' '.join(res) if res else None
def main():
assert tokenization("thequickbrownfox", ['the', 'quick', 'brown', 'fox']) == "the quick brown fox"
assert tokenization("bedbathandbeyond", ['bed', 'bath', 'bedbath', 'and', 'beyond']) == 'bedbath and beyond'
assert tokenization("thequickbrownfox", ['thequickbrownfox']) == "thequickbrownfox"
assert tokenization("thefox", ['thequickbrownfox']) is None
d1 = ['i', 'and', 'like', 'sam', 'sung', 'samsung', 'mobile', 'ice', 'cream', 'icecream', 'man', 'go', 'mango']
assert tokenization("ilikesamsungmobile", d1) == "i like samsung mobile"
assert tokenization("ilikeicecreamandmango", d1) == "i like icecream and mango"
if __name__ == '__main__':
main()
Note that in
tokenization("fox")will end up w/tokenization("o")andtokenization("brown")will also end up w/tokenization("o"). Can we do some optimization there?
Python Solution: https://repl.it/@trsong/Tokenization-Optimziation
def tokenization_recur_with_cache(word, dictionary, cache):
if word not in cache:
cache[word] = tokenization_recur(word, dictionary, cache)
return cache[word]
def tokenization_recur(word, dictionary, cache):
if not word:
return []
for i in xrange(len(word)):
suffix = word[i:]
processed_suffix = [suffix] if not suffix or suffix in dictionary else None
if not processed_suffix: continue
processed_prefix = tokenization_recur_with_cache(word[:i], dictionary, cache)
if processed_prefix is not None:
return processed_prefix + processed_suffix
return None
def tokenization(word, dictionary):
if not word or not dictionary:
return None
else:
res = tokenization_recur_with_cache(word, set(dictionary), {})
return ' '.join(res) if res else None
May 14, 2019 [Medium] Overlapping Rectangles
Questions: You’re given 2 over-lapping rectangles on a plane. For each rectangle, you’re given its bottom-left and top-right points. How would you find the area of their overlap?
My thoughts: If you haven’t seen this question before, don’t worry. You probably should have seen the 1D version of this question. i.e. Find the overlapping length for two intervals. Now think about 2D version of that question, in order to solve the overlapping region, we can project the shape of the graph onto x-axis and y-axis to get x-intersection and y-intersection. The overlapping ara is just product of those two intersections.
Python Solution: https://repl.it/@trsong/Overlapping-Rectangles
# -*- coding: utf-8 -*
class Point(object):
@staticmethod
def x_projection(p1, p2):
return Interval(p1.x, p2.x)
@staticmethod
def y_projection(p1, p2):
return Interval(p1.y, p2.y)
def __init__(self, x, y):
self.x = x
self.y = y
def __eq__(self, other):
return self.x == other.x and self.y == other.y
class Interval(object):
@staticmethod
def intersection(interval1, interval2):
if interval1.end <= interval2.begin or interval2.end <= interval1.begin:
return 0
else:
return min(interval1.end, interval2.end) - max(interval1.begin, interval2.begin)
def __init__(self, begin, end):
self.begin = min(begin, end)
self.end = max(begin, end)
class Rectangle(object):
@staticmethod
def overlapping(r1, r2):
x_projection1 = r1.get_x_projection()
x_projection2 = r2.get_x_projection()
y_projection1 = r1.get_y_projection()
y_projection2 = r2.get_y_projection()
x_intersection = Interval.intersection(x_projection1, x_projection2)
y_intersection = Interval.intersection(y_projection1, y_projection2)
return x_intersection * y_intersection
def __init__(self, bottom_left, top_right):
self.bottom_left = bottom_left
self.top_right = top_right
def get_x_projection(self):
return Point.x_projection(self.bottom_left, self.top_right)
def get_y_projection(self):
return Point.y_projection(self.bottom_left, self.top_right)
def __eq__(self, other):
return self.bottom_left == other.bottom_left and self.top_right == other.top_right
Test strategy: use the following graph to cover all different edge cases
┌───┬───┐ 2,2
│ ┌─┼─┐ │
├─┼─┼─┼─┤
│ └─┼─┘ │
└───┴───┘
-2,-2
def main():
tl = Rectangle(Point(-2,0), Point(0,2))
tr = Rectangle(Point(0,0), Point(2,2))
bl = Rectangle(Point(-2,-2), Point(0,0))
br = Rectangle(Point(0,-2), Point(2,0))
inner = Rectangle(Point(-1,-1), Point(1,1))
outer = Rectangle(Point(-2,-2), Point(2,2))
lst = [tl, tr, bl, br]
origin = Rectangle(Point(0, 0), Point(0, 0))
# Verify all combinations with no overlapping
assert Rectangle.overlapping(origin, origin) == 0
for r in lst + [inner, outer]:
assert Rectangle.overlapping(origin, r) == 0
assert Rectangle.overlapping(r, origin) == 0
for r1 in lst:
for r2 in lst:
if r1 != r2:
assert Rectangle.overlapping(r1, r2) == 0
# Verify all combinations with overlapping = 1
for r in lst:
assert Rectangle.overlapping(r, inner) == 1
assert Rectangle.overlapping(inner, r) == 1
# Verify all combinations with overlapping = 4
assert Rectangle.overlapping(inner, outer) == 4
assert Rectangle.overlapping(outer, inner) == 4
for r in lst:
assert Rectangle.overlapping(r, outer) == 4
assert Rectangle.overlapping(outer, r) == 4
for e in lst + [inner]:
assert Rectangle.overlapping(e, e) == 4
# Verify all combinations with overlapping = 16
assert Rectangle.overlapping(outer, outer) == 16
if __name__ == '__main__':
main()
May 13, 2019 [Medium] Craft Palindrome
Question: Given a string, find the palindrome that can be made by inserting the fewest number of characters as possible anywhere in the word. If there is more than one palindrome of minimum length that can be made, return the lexicographically earliest one (the first one alphabetically).
For example, given the string “race”, you should return “ecarace”, since we can add three letters to it (which is the smallest amount to make a palindrome). There are seven other palindromes that can be made from “race” by adding three letters, but “ecarace” comes first alphabetically.
As another example, given the string “google”, you should return “elgoogle”.
My thoughts: There are two ways to solving this problem. Brute force way VS Dynamic Programming + Tracking Backwards. I was too lazy to post the brute force solution but the idea is to think about each possible piovt positions: there are 2n - 1 of them. And find the smallest among all posible incertions.
e.g. For input = “abcde”, all position of pivot are marked:
| a | b | c | d | e
0 1 2 3 4 5 6 7 8 9
Suppose we choose 1 as pivot, we will need to insert all char in parentheses like the following:
(edcb)abcde
Suppose we choose 2 as pivot, we will need to insert all char in parentheses like the following:
a(cde)bcde(a)
But the brute force solution is NOT efficient in terms of both space and time. As the seach space is huge and a lot of cases are duplicated.
Dynamic Programming + Tracking Backwards Solution
Before think about how to insert character, let’s do that step by step. First consider what’s the minimum number of solutions needed to form a palindrome.
STEP 1: Find Minimum Number of Insertion
Let word[l:r] represents substring of word from index l to index r inclusive. We can break the find_min_insertion(word[l:r]) into:
find_min_insertion(word[l:r-1])find_min_insertion(word[l-1:r])find_min_insertion(word[l-1:r-1])
And we will have the following recursive formula:
If word[l] = word[r] which means the first and last character matches, then we solve the sub-problem:
find_min_insertion(word[l:r]) = find_min_insertion(word[l-1:r-1])
else, we will need to insert 1 charater either to front or back, depends on which sub-problem is smaller
find_min_insertion(word[l:r]) = 1 + min(find_min_insertion(word[l-1:r]), find_min_insertion(word[l:r-1]))
The following code snippet illustrates above recursion
def find_min_insertion(word, left, right):
if left == right:
return 0
elif left == right - 1:
return 0 if word[left] == word[right] else 1
elif word[left] == word[right]:
return find_min_insertion(word, left + 1, right - 1)
else:
drop_left_res = find_min_insertion(word, left + 1, right)
drop_right_res = find_min_insertion(word, left, right - 1)
return 1 + min(drop_left_res, drop_right_res)
STEP 2: Optimize Solution and Store Each Decision We Made
In the recusive solution mentioned above, our solution is not efficient in both time and space. Plus there is no way for us to know what decision we made to get the final value.
So what about using DP to solve this problem?
Well it seems to be a good idea. We define dp[l][r] to be the solution for find_min_insertion(word[l:r]). Then we can use the following formula:
if word[left] == word[right]:
dp[left][right] = dp[left+1][right-1]
else:
dp[left][right] = 1 + min(dp[left+1][right], dp[left][right-1])
But another problem pops up: how do we interate through the 2D array? As dp[left][right] = dp[left+1][right-1]. We cannot do left to right as index l depend on l+1.
A good idea to tackle this problem is the think about how does the recursion tree looks like for previous recursive solution.
e.g. What does recursion looks like for word[0,3]
f(0, 3)
/ | \
/ | \
f(0, 2) f (1, 2) f(1, 3)
/ | \ / | \
f(0, 1) f(1, 1) f(1, 2) f(1, 2) f(2, 2) f(2, 3)
Note that the base case (leaf positon) is either l = r or l = r - 1. We define gap = r - l
Then we find that gap = 2 depends on gap = 1. And gap = 3 depends on gap = 2. So that means we have to solve gap=1 gap=2 gap=3 ... gap=n-2 one-by-one.
Ok, now let’s go back to the issue regarding how we iterate through the dp array.
When gap = 1, we have
dp[0][1], dp[1][2], dp[2][3], dp[3][4]
When gap = 2, we have
dp[0][2], dp[1][3], dp[2][4]
When gap = 3, we have
dp[0][3], dp[1][4]
When gap = 4, we have
dp[0][4]
So you find that r ranges from gap to n-1 and l = r - gap. And here is the DP way to solve this problem:
def find_min_insertion_DP(word):
n = len(word)
dp = [[0 for r in xrange(n)] for c in xrange(n)]
for gap in xrange(1, n):
for right in xrange(gap, n):
left = right - gap
if word[left] == word[right]:
dp[left][right] = dp[left+1][right-1]
else:
dp[left][right] = 1 + min(dp[left+1][right], dp[left][right-1])
return dp[0][n-1]
STEP 3: Tracking Backwards Using the DP Decision Array
Right now we know what is the minimum insertion we have to take. Now we can go backwards and backtracking the decision we made to get such result.
So first of all, let’s take a look at the recursive relation:
if word[left] == word[right]:
dp[left][right] = dp[left+1][right-1]
else:
dp[left][right] = 1 + min(dp[left+1][right], dp[left][right-1])
So if it’s the first case, the we down and left. And if it’s the second case, base on which one is smaller we can determine if we insert word[right] or insert word[left]. And remember the question ask to return the lexicographically earliest one, thus if there is a tie between
dp[left+1][right] and dp[left][right-1]. We will use the lexicographical order of word[left] and word[right] to determine who wins.
You might ask what if we have a tie again between word[left] and word[right]. Then the answer is, we will fall into the first case, dp[left][right] = dp[left+1][right-1].
Python Solution: https://repl.it/@trsong/Craft-Palindrome
def find_min_insertion_DP_helper(word):
n = len(word)
dp = [[0 for r in xrange(n)] for c in xrange(n)]
for gap in xrange(1, n):
for right in xrange(gap, n):
left = right - gap
if word[left] == word[right]:
dp[left][right] = dp[left+1][right-1]
else:
dp[left][right] = 1 + min(dp[left+1][right], dp[left][right-1])
return dp
def craft_palindrome(word):
if not word: return ""
n = len(word)
dp = find_min_insertion_DP_helper(word)
min_insertion = dp[0][n-1]
res = [None] * (n + min_insertion)
left, right = 0, n - 1
updated_left, updated_right = 0, len(res) - 1
while left <= right:
chosen = None
if word[left] == word[right]:
chosen = word[left]
left += 1
right -= 1
else:
drop_left_res = dp[left+1][right]
drop_right_res = dp[left][right-1]
if drop_left_res < drop_right_res or drop_left_res == drop_right_res and word[left] < word[right]:
chosen = word[left]
left += 1
else:
# Either drop_left_res > drop_right_res; Or drop_left_res == drop_right_res and word[left] > word[right]
chosen = word[right]
right -= 1
res[updated_left] = chosen
res[updated_right] = chosen
updated_left += 1
updated_right -= 1
return ''.join(res)
def main():
assert craft_palindrome("") == ""
assert craft_palindrome("a") == "a"
assert craft_palindrome("aa") == "aa"
assert craft_palindrome("race") == "ecarace"
assert craft_palindrome("abcd") == "abcdcba"
assert craft_palindrome("abcda") == "abcdcba"
assert craft_palindrome("abcde") == "abcdedcba"
assert craft_palindrome("google") == "elgoogle"
if __name__ == "__main__":
main()
May 12, 2019 [Medium] Inversion Pairs
Question: We can determine how “out of order” an array A is by counting the number of inversions it has. Two elements
A[i]andA[j]form an inversion ifA[i] > A[j]buti < j. That is, a smaller element appears after a larger element. Given an array, count the number of inversions it has. Do this faster thanO(N^2)time. You may assume each element in the array is distinct.For example, a sorted list has zero inversions. The array
[2, 4, 1, 3, 5]has three inversions:(2, 1),(4, 1), and(4, 3). The array[5, 4, 3, 2, 1]has ten inversions: every distinct pair forms an inversion.
Python Trivial Solution:
def count_inversion_pairs_naive(nums):
inversions = 0
n = len(nums)
for i in xrange(n):
for j in xrange(i+1, n):
inversions += 1 if nums[i] > nums[j] else 0
return inversions
My thoughts: We can start from trivial solution and perform optimization after. In trivial solution basically, we try to count the total number of larger number on the left of smaller number. However, while solving this question, you need to ask yourself, is it necessary to iterate through all combination of different pairs and calculate result?
e.g. For input [5, 4, 3, 2, 1] each pair is an inversion pair, once I know (5, 4) will be a pair, then do I need to go over the remain (5, 3), (5, 2), (5, 1) as 3,2,1 are all less than 4?
So there probably exits some tricks to allow us save some effort to not go over all possible combinations.
Solution 1: Divide and Conquer
Did you notice the following properties?
count_inversion_pairs([5, 4, 3, 2, 1]) = count_inversion_pairs([5, 4]) + count_inversion_pairs([3, 2, 1]) + inversion_pairs_between([5, 4], [3, 2, 1])inversion_pairs_between([5, 4], [3, 2, 1]) = inversion_pairs_between(sorted([5, 4]), sorted([3, 2, 1])) = inversion_pairs_between([4, 5], [1, 2, 3])
This is bascially modified version of merge sort. Consider we break [5, 4, 3, 2, 1] into two almost equal parts: [5, 4] and [3, 2, 1]. Notice such break won’t affect inversion pairs, as whatever on the left remains on the left. However, inversion pairs between [5, 4] and [3, 2, 1] can be hard to count without doing it one-by-one.
If only we could sort them separately as sort won’t affect the inversion order between two lists. i.e. [4, 5] and [1, 2, 3]. Now let’s see if we can find the pattern, if 4 < 1, then 5 should < 1. And we also have 4 < 2 and 4 < 3. We can simply skip all elem > than 4 on each iteration, i.e. we just need to calculate how many elem > 4 on each iteration. This gives us property 2.
And we can futher break [5, 4] into [5] and [4] recursively. This gives us property 1.
Combine property 1 and 2 gives us the modified version of Merge-Sort.
Python Solution1: https://repl.it/@trsong/Inversion-Pairs
def merge(arr, begin, middle, end):
p1 = begin
p2 = middle + 1
mid = middle
inversions = 0
if p2 <= end and arr[mid] <= arr[p2]: return 0
while p1 <= mid and p2 <= end:
if arr[p1] <= arr[p2]:
p1 += 1
else:
inversions += mid - p1 + 1
# shift value by 1 to make room to merge p2 value
value = arr[p2]
for i in xrange(p2, p1, -1):
arr[i] = arr[i-1]
arr[p1] = value
p1 += 1
p2 += 1
mid += 1
return inversions
def merge_sort(arr, begin, end):
if begin >= end: return 0
mid = begin + (end - begin) / 2
left_sub_inversions = merge_sort(arr, begin, mid)
right_sub_inversions = merge_sort(arr, mid + 1, end)
current_inversions = merge(arr, begin, mid, end)
return left_sub_inversions + right_sub_inversions + current_inversions
def count_inversion_pairs(nums):
return merge_sort(nums, 0, len(nums) - 1)
def main():
# For list in descending order, each pair forms an inversion pair, so we have n(n-1)/2 = 5 * 4 / 2 = 10
assert count_inversion_pairs([5, 4, 3, 2, 1]) == 10
assert count_inversion_pairs([2, 4, 1, 3, 5]) == 3
assert count_inversion_pairs([1, 2, 3]) == 0
assert count_inversion_pairs([1, 1, 1, 1]) == 0
assert count_inversion_pairs([1]) == 0
assert count_inversion_pairs([]) == 0
if __name__ == '__main__':
main()
Solution 2: Counting number of smaller elements efficiently
In the trivial solution above, we scan through all different combination of elements. However, is there any way we can sort of cache the previous counting result. i.e. Going backwards from the list and keep track of number of smaller element on the left.
e.g. Process from right to left of [1, 2, 3, 4, 5]
- Process 5, no smaller elem found
- Process 4, no smaller elem found
- Process 3, no smaller elem found
- Process 2, no smaller elem found
- Process 1, no smaller elem found Total Number of inversions: 0
e.g. Process from right to left of [5, 4, 3, 2, 1]
- Process 1, no smaller elem found
- Process 2, found 1 candidate which is 1, possible inversion (2, 1)
- Process 3, found 2 candidates: 1 and 2. possible inversion (3, 2), (3, 1)
- Process 4, found 3 candidates: 1, 2 and 3. possible inversion (4, 3), (4, 2), (4, 1)
- Process 5, found 4 candidates: 1, 2, 3, 4. possible inversion (5, 4), (5, 3), (5, 2), (5,1) Total Number of inversions: 0 + 1 + 2 + 3 + 4 = 10
Notice that we don’t need to keep track of exact smaller number, just storing those numbers are sufficient. And we happen to have a powerful data structure that by giving a value, it can quickly returns number of smaller elements. Such data structure is called Binary Indexed Tree (BIT) and it can do well in range queries. i.e. calculate range sum.
How?
Think about an array A where A[i] represents number of elem smaller than i. Then counting the number of smaller-than-target elem is sum of A[0], A[1], …, A[target-1]. And BIT can do well in range queries.
Python Solution2: https://repl.it/@trsong/Inversion-Pairs2
class PrefixSum(object):
"""PrefixSum provide an efficient way to update and calculate range sum on the fly"""
@staticmethod
def last_bit(num):
return num & -num
def __init__(self, size):
self._BITree = [0] * (size + 1)
def get_sum(self, i):
"""Get sum of value from index 0 to i """
# BITree starts from index 1
index = i + 1
res = 0
while index > 0:
res += self._BITree[index]
index -= PrefixSum.last_bit(index)
return res
def update(self, i, delta):
"""Update the sum by add delta on top of result"""
# BITree starts from index 1
index = i + 1
while index < len(self._BITree):
self._BITree[index] += delta
index += PrefixSum.last_bit(index)
def count_inversion_pairs2(nums):
if not nums: return 0
max_value = max(nums)
# Store number of elem less than current value in prefix_sum
prefix_sum = PrefixSum(max_value)
inversions = 0
for i in xrange(len(nums) - 1, -1, -1):
# We count inversions backwards. For each elem, we use prefix sum to calculate number of elem less than current value
current_value = nums[i]
inversions += prefix_sum.get_sum(current_value - 1)
prefix_sum.update(current_value, 1)
return inversions
May 11, 2019 LC 42 [Hard] Trapping Rain Water
Question: Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
My thoughts: This question can be solved w/ pre-record left & right boundary as well as with 2 pointers. Both solution take O(n) time. However, first solution requires more memory than second one.
Solution 1: Pre-record Left & Right Boundary
Total water accumulation equals sum of each position’s accumulation. For any position at index i, the reason why current position has water accumulation is due to the fact that there exist l < i such that water_height[l] > water_height[i] as well as i < r such that water_height[r] > water_height[i].
We probably don’t care about what l, r are. However, we do care about how much each position can accumulate at maximum. min(left_boundary[i], right_boundary[i]) - water_height[i]. Where left_boundary represents max height on the left of i and right_boundary represents max height on the right of i.
Use the following as example:

| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| water_height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
| left_boundary | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 |
| right_boundary | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 0 |
| accumulation(blue reigon) | 0 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 0 |
Python Solution: https://repl.it/@trsong/trappingRainWater
def trapping_rain_water_solver(water_height):
n = len(water_height)
left_boundary = [0] * n
right_boundary = [0] * n
left = 0
right = 0
for i in xrange(n):
left_boundary[i] = left
right_boundary[n-1-i] = right
left = max(left, water_height[i])
right = max(right, water_height[n-i-1])
sum = 0
for i in xrange(n):
# How much water can be accumulated at index i is depend on max boundary height on the left and max boundary on the right.
sum += max(0, min(left_boundary[i], right_boundary[i]) - water_height[i])
return sum
def main():
assert trapping_rain_water_solver([0,1,0,2,1,0,1,3,2,1,2,1]) == 6
assert trapping_rain_water_solver([1, 1, 1, 2]) == 0
assert trapping_rain_water_solver([1, 1, 1, 1]) == 0
assert trapping_rain_water_solver([2, 1, 1, 1]) == 0
assert trapping_rain_water_solver([]) == 0
assert trapping_rain_water_solver([1, 1, 2, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 2, 1]) == 8
assert trapping_rain_water_solver([3, 2, 1, 2, 3]) == 4
if __name__ == '__main__':
main()
Solution 2: 2 pointers
Maintain two pointers and always move pointer w/ smaller height to the other one. How this works is because if left pointer is smaller: water_height[left] < water_height[right], then there must be an index k between left and right represents local right boundary such that its value water_height[left] < water_height[k] <= water_height[right]. Note that heights between left and k is either increasing or decresing. We can calculate water accumulation between left and k. And vice versa when right pointer is smaller.
Use the following as example:

| Iteration | Direction | Accumulation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | start | 0 | ||||||||||
| 2 | 0 | 1 | 1 | -> | 0 | |||||||||
| 3 | 0 | 1 | 0 | 2 | 1 | -> | 1 | |||||||
| 4 | 0 | 1 | 0 | 2 | 2 | 1 | -> | 0 | ||||||
| 5 | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | -> | 1 + 2 + 1 = 4 | ||
| 6 | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 | <- | 1 |
total: 1 + 4 + 1 = 6
def trapping_rain_water_solver2(water_height):
lo = 0
hi = len(water_height) - 1
sum = 0
while lo < hi:
left_boundary = water_height[lo]
right_boundary = water_height[hi]
if left_boundary < right_boundary:
# If left_boundary < right_boundary, there exists a local_right_bounary while we are moving from left to right
# such that left_boundary < local_right_bounary <= right_boundary
while lo < hi and left_boundary >= water_height[lo]:
# Accumulate water between left_boundary and local_right_bounary
sum += left_boundary - water_height[lo]
lo += 1
else:
# If left_boundary >= right_boundary, there exists a local_left_boundary while moveing from right to left
# such that left_boundary <= local_left_bounary < right_boundary
while lo < hi and right_boundary >= water_height[hi]:
# Accumulate water between right_boundary and local_left_bounary
sum += right_boundary - water_height[hi]
hi -= 1
return sum
May 10, 2019 [Hard] Execlusive Product
Question: Given an array of integers, return a new array such that each element at index i of the new array is the product of all the numbers in the original array except the one at i.
For example, if our input was [1, 2, 3, 4, 5], the expected output would be [120, 60, 40, 30, 24]. If our input was [3, 2, 1], the expected output would be [2, 3, 6].
Follow-up: what if you can’t use division?
My thoughts: For an input array [a[0], a[1], a[2], a[3], a[4]], what will be the value for output at index i?
It should be res[i] = a[0] * a[1] * ... a[i-1] * a[i+1] * ... * a[n-1], which basically equals res[i] = (a[0] * a[1] * ... * a[i-1]) * (a[i+1] * ... * a[n-1]). We can use one array to store all left products and another array for right products.
eg. left_execlusive_product[i] = a[0] * a[1] * ... * a[i-1] and right_execlusive_product[i] = a[i+1] * ... * a[n-1]. Thus res[i] = left_execlusive_product[i] * right_execlusive_product[i]
Note that left_execlusive_product[i] = left_execlusive_product[i-1] * a[i-1] so that we can calculate left_execlusive_product quite easily. Which take O(N) time. Similarly, right_execlusive_product can also calculate within O(N) time.
Python Solution: https://repl.it/@trsong/execlusiveproduct
def execlusive_product(nums):
if not nums: return []
n = len(nums)
left_execlusive_product = [0] * n
right_execlusive_product = [0] * n
left = 1
for i in xrange(n):
left_execlusive_product[i] = left
left *= nums[i]
right = 1
for j in xrange(n - 1, -1, -1):
right_execlusive_product[j] = right
right *= nums[j]
return [left_execlusive_product[i] * right_execlusive_product[i] for i in xrange(n)]
def main():
assert execlusive_product([1, 2, 3, 4, 5]) == [120, 60, 40, 30, 24]
assert execlusive_product([]) == []
assert execlusive_product([2]) == [1]
assert execlusive_product([3, 2]) == [2, 3]
if __name__ == '__main__':
main()
Note: We can further optimize the code by combining two loops into one.
def execlusive_product2(nums):
# one pass optimization
if not nums: return []
n = len(nums)
left = 1
right = 1
res = [1] * n
for i in xrange(n):
res[i] *= left
res[n-1-i] *= right
left *= nums[i]
right *= nums[n-1-i]
return res
May 9, 2019 [Easy] Grid Path
Question: You are given an M by N matrix consisting of booleans that represents a board. Each True boolean represents a wall. Each False boolean represents a tile you can walk on.
Given this matrix, a start coordinate, and an end coordinate, return the minimum number of steps required to reach the end coordinate from the start. If there is no possible path, then return null. You can move up, left, down, and right. You cannot move through walls. You cannot wrap around the edges of the board.
For example, given the following board:
[
[F, F, F, F],
[T, T, F, T],
[F, F, F, F],
[F, F, F, F]
]
and start = (3, 0) (bottom left) and end = (0, 0) (top left), the minimum number of steps required to reach the end is 7, since we would need to go through (1, 2) because there is a wall everywhere else on the second row.
My thoughts: Use BFS from start to end. Each layer we proceed will contribute to distance by 1. e.g. If end is one of start’s level-7 descendant then the distance will be 7.
Python Solution1: https://repl.it/@trsong/gridpath
class Position(object):
def __init__(self, row, col):
self.row = row
self.col = col
def __repr__(self):
return "(%d, %d)" % (self.row, self.col)
def __hash__(self):
return hash((self.row, self.col))
def __eq__(self, other):
return self.row == other.row and self.col == other.col
def grid_path(grid_wall, start, end):
num_row = len(grid_wall)
num_col = len(grid_wall[0])
distance = 0
queue = [start]
visited = set()
while queue:
level_size = len(queue)
for i in xrange(level_size):
current = queue.pop(0)
if current in visited: continue
if current == end:
return distance
visited.add(current)
top = Position(current.row - 1, current.col) if current.row > 0 else None
if top and not grid_wall[top.row][top.col] and top not in visited:
queue.append(top)
left = Position(current.row, current.col - 1) if current.col > 0 else None
if left and not grid_wall[left.row][left.col] and left not in visited:
queue.append(left)
bottom = Position(current.row + 1, current.col) if current.row < num_row - 1 else None
if bottom and not grid_wall[bottom.row][bottom.col] and bottom not in visited:
queue.append(bottom)
right = Position(current.row, current.col + 1) if current.col < num_col - 1 else None
if right and not grid_wall[right.row][right.col] and right not in visited:
queue.append(right)
distance += 1
return None
def main():
F = False
T = True
wall_map1 = [
[F, F, F, F],
[T, T, F, T],
[F, F, F, F],
[F, F, F, F]
]
assert grid_path(wall_map1, Position(0, 0), Position(3, 0)) == 7
wall_map2 = [
[F, F, F, F],
[T, T, T, T],
[F, F, F, F],
[F, F, F, F]
]
assert grid_path(wall_map2, Position(0, 0), Position(3, 0)) is None
wall_map3 = [
[F, F, F, F, T, F, F, F],
[T, T, T, F, T, F, T, T],
[F, F, F, F, T, F, F, F],
[F, T, T, T, T, T, T, F] ,
[F, F, F, F, F, F, F, F]
]
assert grid_path(wall_map3, Position(0, 0), Position(0, 7)) == 25
wall_map4 = [[F, F]]
assert grid_path(wall_map4, Position(0, 0), Position(0, 1)) == 1
if __name__ == '__main__':
main()
Note: This question can also be solved use Bidirectional BFS (2-way BFS).
Python Solution2: https://repl.it/@trsong/gridpath2
def search(grid_wall, queue, visited, other_visited):
"""Search all elem in queue to find exist elem in other_visited. Add all neighbors to queue after."""
num_row = len(grid_wall)
num_col = len(grid_wall[0])
level_size = len(queue)
for i in xrange(level_size):
current = queue.pop(0)
if current in visited: continue
if current in other_visited:
return current
visited.add(current)
top = Position(current.row - 1, current.col) if current.row > 0 else None
if top and not grid_wall[top.row][top.col] and top not in visited:
queue.append(top)
left = Position(current.row, current.col - 1) if current.col > 0 else None
if left and not grid_wall[left.row][left.col] and left not in visited:
queue.append(left)
bottom = Position(current.row + 1, current.col) if current.row < num_row - 1 else None
if bottom and not grid_wall[bottom.row][bottom.col] and bottom not in visited:
queue.append(bottom)
right = Position(current.row, current.col + 1) if current.col < num_col - 1 else None
if right and not grid_wall[right.row][right.col] and right not in visited:
queue.append(right)
return None
def grid_path2(grid_wall, start, end):
iteration = 0
start_visited = set()
end_visited = set()
start_queue = [start]
end_queue = [end]
while start_queue and end_queue:
# Forward search and add neighbors
if search(grid_wall, start_queue, start_visited, end_visited):
return 2 * iteration - 1
# Backward search and add neighbors
if search(grid_wall, end_queue, end_visited, start_visited):
return 2 * iteration
iteration += 1
return None
May 8, 2019 LC 130 [Medium] Surrounded Regions
Question: Given a 2D board containing ‘X’ and ‘O’ (the letter O), capture all regions surrounded by ‘X’. A region is captured by flipping all ‘O’s into ‘X’s in that surrounded region.
Example:
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
X X X X
X X X X
X X X X
X O X X
Explanation:
Surrounded regions shouldn’t be on the border, which means that any ‘O’ on the border of the board are not flipped to ‘X’. Any ‘O’ that is not on the border and it is not connected to an ‘O’ on the border will be flipped to ‘X’. Two cells are connected if they are adjacent cells connected horizontally or vertically.
My thoughts: There are mutiple ways to solve this question. Solution 1 use DFS and Solution 2 use Union-Find.
Solution 1: for all ‘O’ cells connect to boundary of the grid, temporarily mark them as ‘-‘. And then scan through entire grid, replace ‘O’ with ‘X’ and ‘-‘ with ‘O’
- Orginal Grid:
[ ['X', 'O', 'X', 'X', 'O'], ['X', 'X', 'O', 'O', 'X'], ['X', 'O', 'X', 'X', 'O'], ['O', 'O', 'O', 'X', 'O'] ] - Replace all ‘O’ connect to bounary as ‘-‘
[ ['X', '-', 'X', 'X', '-'], ['X', 'X', 'O', 'O', 'X'], ['X', '-', 'X', 'X', '-'], ['-', '-', '-', 'X', '-'] ] - Replace ‘O’ with ‘X’ and ‘-‘ with ‘O’
[ ['X', 'O', 'X', 'X', 'O'], ['X', 'X', 'X', 'X', 'X'], ['X', 'O', 'X', 'X', 'O'], ['O', 'O', 'O', 'X', 'O'] ]
Python Solution 1: https://repl.it/@trsong/surroundedregionsdfs
class SurroundedReigonSolver(object):
def __init__(self, grid):
self._grid = grid
self._num_row = len(grid)
self._num_col = len(grid[0])
def _indexToPosition(self, row, col):
return row * self._num_col + col
def _positionToIndex(self, pos):
return (pos / self._num_col, pos % self._num_col)
def _dfs_search_replace(self, visited, source_pos, target):
r, c = self._positionToIndex(source_pos)
source = self._grid[r][c]
stack = [source_pos]
while stack:
current = stack.pop()
r, c = self._positionToIndex(current)
# process current cell
if current not in visited and self._grid[r][c] == source:
self._grid[r][c] = target
visited.add(current)
# Check and add bottom to stack
if r < self._num_row - 1:
stack.append(self._indexToPosition(r + 1, c))
# Check and add right to stack
if c < self._num_col - 1:
stack.append(self._indexToPosition(r, c + 1))
# Check and add top to stack
if r > 0:
stack.append(self._indexToPosition(r - 1, c))
# Check and add top left to stack
if c > 0:
stack.append(self._indexToPosition(r, c - 1))
def solve(self):
# Mark all edge-connected 'O' cells as '-'
visited = set()
for i in xrange(self._num_col):
if self._grid[0][i] == 'O':
self._dfs_search_replace(visited, self._indexToPosition(0, i), '-')
if self._grid[self._num_row - 1][i] == 'O':
self._dfs_search_replace(visited, self._indexToPosition(self._num_row - 1, i), '-')
for j in xrange(self._num_row):
if self._grid[j][0] == 'O':
self._dfs_search_replace(visited, self._indexToPosition(j, 0), '-')
if self._grid[j][self._num_col - 1] == 'O':
self._dfs_search_replace(visited, self._indexToPosition(j, self._num_col - 1), '-')
# Replace all 'O' with 'X' and '-' with 'O'
for r in xrange(self._num_row):
for c in xrange(self._num_col):
if self._grid[r][c] == 'O':
self._grid[r][c] = 'X'
elif self._grid[r][c] == '-':
self._grid[r][c] = 'O'
return self._grid
def main():
grid1 = [
['X', 'X', 'X', 'X'],
['X', 'O', 'O', 'X'],
['X', 'X', 'O', 'X'],
['X', 'O', 'X', 'X']
]
solved_grid1 = [
['X', 'X', 'X', 'X'],
['X', 'X', 'X', 'X'],
['X', 'X', 'X', 'X'],
['X', 'O', 'X', 'X']
]
solver = SurroundedReigonSolver(grid1)
assert solver.solve() == solved_grid1
grid2 = [
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O']
]
solved_grid2 = [
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O']
]
solver2 = SurroundedReigonSolver(grid2)
assert solver2.solve() == solved_grid2
grid3 = [
['X', 'O', 'X', 'X', 'O'],
['X', 'X', 'O', 'O', 'X'],
['X', 'O', 'X', 'X', 'O'],
['O', 'O', 'O', 'X', 'O']
]
solved_grid3 = [
['X', 'O', 'X', 'X', 'O'],
['X', 'X', 'X', 'X', 'X'],
['X', 'O', 'X', 'X', 'O'],
['O', 'O', 'O', 'X', 'O']
]
solver3 = SurroundedReigonSolver(grid3)
assert solver3.solve() == solved_grid3
if __name__ == '__main__':
main()
Solution 2: There is a special data-structure called Union-Find that allow us to quickly determine if two cells are CONNECTED or not.
The idea of Union-Find is as the following:
-
Suppose we have an array:
[0, 1, 2, 3, 4, 5]represents 5 different cells. -
And we create a parent array which initialized to be
[-1, -1, -1, -1, -1, -1]. That means all cell’s parent is null and none of the cells are connected - they have no shared parent. -
Now if we want to connect cell 0 and cell 5 by marking cell 0's parent as 5 (we call this action “Union”). Parent array will become
[5, -1, -1, -1, -1, -1]. -
And if we also connect 3 and 0 so that all of 0,3,5 are connected. we will have parent array looks like
[5, -1, -1, 0, -1, -1]. -
Now we defined
is_connected(index1, index2)if they all share the same root. In our example 0,3,5 are connected and everything else is connected to itself separately. -
Since `parent[0] == 5` and `parent[3] == parent[0] == 5` and 5 has not parent indicates it is the root. (We call the action of retrieving parent recursively: “Find”)
-
By keeping calling union and find on different cells will allow us to connect those cells. And quickly tell if two cells are connected.
The way we use Union-Find to conquer this question looks like the following:
- Step 1: Init the parent arry:
Orginal Grid:
[ ['X', 'O', 'X', 'X', 'O'], ['X', 'X', 'O', 'O', 'X'], ['X', 'O', 'X', 'X', 'O'], ['O', 'O', 'O', 'X', 'O'] ]parent array
[ [-1, -1, -1, -1, -1], [-1, -1, -1, -1, -1], [-1, -1, -1, -1, -1], [-1, -1, -1, -1, -1] [-1] <----------------- we also create a secret cell for future use ] -
Step 2: Now connect all connected ‘O’ use Union-Find
parent array: instead of using parent index, I use letter to represent different connected region
[ [-1, A, -1, -1, B], [-1, -1, C, C, -1], [-1, E, -1, -1, D], [ E, E, E, -1, D] [-1] <----------------- In the next step we will take advantage of this cell ] - Step 3: Let’s connect the secret cell to all edge-connected ‘O’ cells
parent array: instead of using parent index, I use letter to represent different connected region
[
[-1, O, -1, -1, O],
[-1, -1, C, C, -1],
[-1, O, -1, -1, O],
[ O, O, O, -1, O]
[ O] <----------------- this cell is used to connect to all 'O' on the edge of the grid
]
-
Step 4: Replace all ‘O’ with ‘X’, except for connected-to-secret-spot ones
[ ['X', 'O', 'X', 'X', 'O'], ['X', 'X', 'X', 'X', 'X'], ['X', 'O', 'X', 'X', 'O'], ['O', 'O', 'O', 'X', 'O'] ]Note for my implementation of union-find, I flatten the parent 2D array into 1D array.
Python Solution 2: https://repl.it/@trsong/surroundedregionsunionfind
class SurroundedReigonSolver(object):
def __init__(self, grid):
self._grid = grid
self._num_row = len(grid)
self._num_col = len(grid[0])
self._parent = [-1] * (self._num_row * self._num_col + 1)
def _indexToPosition(self, row, col):
return row * self._num_col + col
def _find(self, pos):
if self._parent[pos] < 0:
return pos
else:
return self._find(self._parent[pos])
def _union(self, pos1, pos2):
parent1 = self._find(pos1)
parent2 = self._find(pos2)
if parent1 != parent2:
self._parent[pos2] = pos1
def _is_connected(self, pos1, pos2):
return self._find(pos1) == self._find(pos2)
def solve(self):
# Scan through the grid to connect all 'O'
for r in xrange(self._num_row):
for c in xrange(self._num_col):
current_pos = self._indexToPosition(r, c)
# Note, as we are moving right and down, we only need to check top and left
if self._grid[r][c] == 'O':
if r > 0 and self._grid[r-1][c] == 'O':
self._union(current_pos, self._indexToPosition(r-1, c))
if c > 0 and self._grid[r][c-1] == 'O':
self._union(current_pos, self._indexToPosition(r, c-1))
# Connect all edge-connnected 'O' cell to this secret_pos
secret_pos = self._num_row * self._num_col
for i in xrange(self._num_col):
if self._grid[0][i] == 'O':
self._union(secret_pos, self._indexToPosition(0, i))
if self._grid[self._num_row-1][i] == 'O':
self._union(secret_pos, self._indexToPosition(self._num_row-1, i))
for j in xrange(self._num_row):
if self._grid[j][0] == 'O':
self._union(secret_pos, self._indexToPosition(j, 0))
if self._grid[j][self._num_col-1] == 'O':
self._union(secret_pos, self._indexToPosition(j, self._num_col-1))
for r in xrange(self._num_row):
for c in xrange(self._num_col):
# Only replace 'O' with 'X' unless it's connected to secret_pos
if self._grid[r][c] == 'O' and not self._is_connected(secret_pos, self._indexToPosition(r, c)):
self._grid[r][c] = 'X'
return self._grid
Optimization for Solution 2: Union-find can be optimized w/ :
- Find Optimization: Flatten the parent array on the fly
- Union Optimization: Balance number of children for the same root
By doing the following optimization will allow us to have a faster is_connected(pos1, pos2) check.
class SurroundedReigonSolver2(object):
def __init__(self, grid):
self._grid = grid
self._num_row = len(grid)
self._num_col = len(grid[0])
self._parent = range(self._num_row * self._num_col + 1)
self._parent_weight = [0] * len(self._parent)
def _find(self, pos):
if self._parent[pos] == pos:
return pos
else:
# we flatten the path from current node to root
root = self._find(self._parent[pos])
self._parent[pos] = root
return root
def _union(self, pos1, pos2):
parent1 = self._find(pos1)
parent2 = self._find(pos2)
if parent1 != parent2:
# Note we always connect light branch to heavy branch
# eg. 1 <- 2 <- 3 <- 5 and 6 <- 7
# we will have 1 <- 2 <- 3 <- 5 and 1 <- 6 <- 7
if self._parent_weight[parent1] == self._parent_weight[parent2]:
self._parent[parent1] = pos2
self._parent_weight[parent2] += 1
elif self._parent_weight[parent1] < self._parent_weight[parent2]:
# parent2 has more nodes recognize it as root
self._parent[parent1] = pos2
else:
# parent1 has more nodes recognize it as root
self._parent[parent2] = pos1
def _is_connected(self, pos1, pos2):
return self._find(pos1) == self._find(pos2)
May 7, 2019 [Hard] Largest Sum of Non-adjacent Numbers
Question: Given a list of integers, write a function that returns the largest sum of non-adjacent numbers. Numbers can be 0 or negative.
For example,
[2, 4, 6, 2, 5]should return 13, since we pick 2, 6, and 5.[5, 1, 1, 5]should return 10, since we pick 5 and 5.Follow-up: Can you do this in O(N) time and constant space?
My thoughts: Try to find the pattern by examples:
Let keep it simple first, just assume all elements are positive:
[] => 0 # Sum of none equals 0
[2] => 2 # the only elem is 2
[2, 4] => 4 # 2 and 4 we will choose 4
[2, 4, 6] => 2+6 => 8 # The pattern is eithe choose all odd index numbers or all even index numbers. eg. [_, 4, _] vs [2, _, 6]. We choose 2,6 which gives 8. If it's [1, 99, 1], we will choose 99 instead.
[2, 4, 6, 2] => [_, 4, _, 2] vs [2, _, 6, _] => 6 vs 8 => 8
# If we let f[lst] represents the max non-adjacent sum when input array is lst
f[2, 4, 6] = max { f[2] + 6, f[4] } = max{6, 8} = 8
f[2, 4, 6, 2] = max { f[2, 4] + 2, f[2, 4, 6] } = max{4, 8} = 8
f[2, 4, 6, 2, 5] = max {f[2, 4, 6] + 5, f[2, 4, 6, 2]} = max{8 + 5, 8} = 13
f[a1, a2, ...., an] = max {f[a1, ..., an-2] + an, f[a1, a2, ..., an-1]}
What if one of the element is negative? i.e. [-1, -1, 1]
# if we continue apply the formula above, we will end up minus a number from max sum
f[-1, -1, 1] = max{f[-1] + 1, f[-1, -1]} = max{-1+1, -1} = 0
# we can choose to not include that number
#f[-1, -1, 1] should equal to 1
f[-1, -1, 1] = max{f[-1] + 1, f[-1, -1], 1} = max{-1+1, -1, 1} = 1
# As all previous sum chould be a negative number, if that's the case, we can just include the positive number.
f[a1, a2, ...., an] = max {f[a1, ..., an-2] + an, f[a1, a2, ..., an-1], an}
# If we let dp[n] represents the max non-adjacent sum when input size is n, then
dp[i] = max(dp[i-1], dp[i-2] + numbers[i-1], numbers[i-1])
# dp[n] will be the answer to f[a0, a2, ...., an-1]
Python Solution: https://repl.it/@trsong/nonadjacentsum
def non_adjacent_sum(numbers):
# Let dp[n] represents the max non-adjacent sum when input size is n.
# Now let's focusing on the number with index n - 1:
# * If that number is negative, then including this number won't do us any good. i.e. dp[n] = dp[n - 1]
# * If that number is positive, then we either include this number, i.e. dp[n] = dp[n-2] + numbers[n-1]
# or not include this number, i.e. dp[n] = dp[n-1]
# * Moreover, what if dp[n-1] and dp[n-2] are all negative, but the number with index n - 1 is positive.
# Then we will need to consider dp[n] = numbers[n-1]
if not numbers: return 0
if len(numbers) == 1: return numbers[0]
n = len(numbers)
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = numbers[0]
dp[2] = max(numbers[0], numbers[1])
for i in xrange(3, n + 1):
dp[i] = max(dp[i-1], dp[i-2] + numbers[i-1], numbers[i-1])
return dp[n]
def non_adjacent_sum2(numbers):
# Solution satisfies O(N) time and constant space
if not numbers: return 0
if len(numbers) == 1: return numbers[0]
prev_prev_dp = numbers[0]
prev_dp = max(numbers[0], numbers[1])
current = prev_dp
for i in xrange(3, len(numbers) + 1):
current = max(prev_dp, prev_prev_dp + numbers[i-1], numbers[i-1])
prev_prev_dp, prev_dp = prev_dp, current
return current
def main():
assert non_adjacent_sum2([]) == 0
assert non_adjacent_sum2([2]) == 2
assert non_adjacent_sum2([2, 4]) == 4
assert non_adjacent_sum2([2, 4, -1]) == 4
assert non_adjacent_sum2([2, 4, -1, 0]) == 4
assert non_adjacent_sum2([2, 4, 6, 2, 5]) == 13
assert non_adjacent_sum2([5, 1, 1, 5]) == 10
assert non_adjacent_sum2([-1, -2, -3, -4]) == -1
assert non_adjacent_sum2([1, -1, 1, -1]) == 2
assert non_adjacent_sum2([1, -1, -1, -1]) == 1
assert non_adjacent_sum2([1, 1, 1, 1, 1]) == 3
assert non_adjacent_sum2([1, -1, -1, 1, 2]) == 3
assert non_adjacent_sum2([1, -1, -1, 2, 1]) == 3
if __name__ == '__main__':
main()
May 6, 2019 [Hard] Climb Staircase (Continued)
Question: There exists a staircase with N steps, and you can climb up either 1 or 2 steps at a time. Given N, write a function that PRINT out all possible unique ways you can climb the staircase. The ORDER of the steps matters.
For example, if N is 4, then there are 5 unique ways (accoding to May 5’s question). This time we print them out as the following:
1, 1, 1, 1
2, 1, 1
1, 2, 1
1, 1, 2
2, 2
What if, instead of being able to climb 1 or 2 steps at a time, you could climb any number from a set of positive integers X?
For example, if N is 6, and X = {2, 5}. You could climb 2 or 5 steps at a time. Then there is only 1 unique way, so we print the following:
2, 2, 2
My thoughts: The only way to figure out each path is to manually test all outcomes. However, certain cases are invalid (like exceed the target value while climbing) so we try to modify certain step until its valid. Such technique is called Backtracking.
We may use recursion to implement backtracking, each recursive step will create a separate branch which also represent different recursive call stacks. Once the branch is invalid, the call stack will bring us to a different branch, i.e. backtracking to a different solution space.
For example, if N is 4, and feasible steps are [1, 2], then there are 5 different solution space/path. Each node represents a choice we made and each branch represents a recursive call.
Note we also keep track of the remaining steps while doing recursion.
├ 1
│ ├ 1
│ │ ├ 1
│ │ │ └ 1 SUCCEED
│ │ └ 2 SUCCEED
│ └ 2
│ └ 1 SUCCEED
└ 2
├ 1
│ └ 1 SUCCEED
└ 2 SUCCEED
If N is 6 and fesible step is [5, 2]:
├ 5 FAILURE
└ 2
└ 2
└ 2 SUCCEED
Python Solution: https://repl.it/@trsong/climbStairs2
SEPARATOR = ", "
def climbStairsRecur(feasible, remain, path, res):
global SEPARATOR
# Once climbed all staircases, include this path
if remain == 0:
res.append(SEPARATOR.join(map(str, path)))
return res
else:
# Test all feasible steps and if it works then proceed
for step in feasible:
if remain - step >= 0:
newPath = path + [step]
# What if we choose this path, do recursion on remaining staircases
climbStairsRecur(feasible, remain - step, newPath, res)
def climbStairs2(n, feasibleStairs):
res = []
climbStairsRecur(feasibleStairs, n, [], res)
return res
def testResult(res, expected):
return sorted(res) == sorted(expected)
def main():
assert testResult(climbStairs2(5, [1, 3, 5]), [
"1, 1, 1, 1, 1",
"3, 1, 1",
"1, 3, 1",
"1, 1, 3",
"5"])
assert testResult(climbStairs2(4, [1, 2]), [
"1, 1, 1, 1",
"2, 1, 1",
"1, 2, 1",
"1, 1, 2",
"2, 2"
])
assert testResult(climbStairs2(9, []), [])
assert testResult(climbStairs2(42, [42]), ["42"])
assert testResult(climbStairs2(4, [1, 2, 3, 4]), [
"1, 1, 1, 1",
"1, 1, 2",
"1, 2, 1",
"1, 3",
"2, 1, 1",
"2, 2",
"3, 1",
"4"
])
assert testResult(climbStairs2(99, [7]), [])
if __name__ == '__main__':
main()
May 5, 2019 [Medium] Climb Staircase
Question: There exists a staircase with N steps, and you can climb up either 1 or 2 steps at a time. Given N, write a function that returns a number represents the total number of unique ways you can climb the staircase.
For example, if N is 4, then there are 5 unique ways:
- 1, 1, 1, 1
- 2, 1, 1
- 1, 2, 1
- 1, 1, 2
- 2, 2
My thoughts: Imagine when you step on the nth staircase, what could be the previous move you made to get to the nth staircase. You only have two ways:
- Either, you were on (n-1)th staircase and you climbed 1 staircase next
- Or, you were on (n-2)th staircase and you climbed 2 staircase next So the total number of way to climb n staircase depends on how many ways to climb n-1 staircases + how many ways to climb n-2 staircases.
Note: Did you notice the solution forms a Fibonacci Sequence? Well same optimization tricks also work for this question.
Python Solutions: https://repl.it/@trsong/climbStairs
def climbStairs(n):
# Let dp[n] represent the number of ways to climb n stairs, then we will have
# dp[n] = dp[n-1] + dp[n-2]
# Because in order to get to n-th stair case, you can only reach from the (n-1)th or (n-2)th.
# Which have dp[n-1] and dp[n-2] of ways separately.
dp = [0] * max(n + 1, 3)
dp[1] = 1 # climb 1
dp[2] = 2 # climb 1, 1 or 2
for i in xrange(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
def main():
assert climbStairs(1) == 1
assert climbStairs(2) == 2
assert climbStairs(3) == 3
assert climbStairs(4) == 5
assert climbStairs(5) == 8
assert climbStairs(6) == 13
if __name__ == '__main__':
main()
May 4, 2019 [Easy] Power Set
Question: The power set of a set is the set of all its subsets. Write a function that, given a set, generates its power set.
For example, given a set represented by a list
[1, 2, 3], it should return[[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]representing the power set.
My thoughts: There are multiple ways to solve this problem. Solution 1 & 2 use recursion that build subsets incrementally. While solution 3, only cherry pick elem based on binary representation.
Solution 1 & 2: Let’s calculate the first few terms and try to figure out the pattern
powerSet([]) => [[]]
powerSet([1]) => [[], [1]]
powerSet([1, 2]) => [[], [1], [2], [1, 2]]
powerSet([1, 2, 3]) => [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]] which is powerSet([1, 2]) + append powerSet([1, 2]) with new elem 3
...
powerSet([1, 2, ..., n]) => powerSet([1, 2, ..., n - 1]) + append powerSet([1, 2, ..., n - 1]) with new elem n
Solution 3: the total number of subsets eqauls $2^n$. Notice that we can use binary representation to represent which elem to cherry pick. e.g. powerSet([1, 2, 3]). 000 represent [], 010 represents [2] and 101 represents [1, 3].
Binary representation of selection has $|{1, 2, 3}| = 2^3 = 8$ outcomes
000 => []
001 => [3]
010 => [2]
011 => [2, 3]
100 => [1]
101 => [1, 3]
110 => [1, 2]
111 => [1, 2, 3]
Python Solution: Link: https://repl.it/@trsong/powerSet
def powerSet(inputSet):
if not inputSet:
return [[]]
else:
subsetRes = powerSet(inputSet[1:])
return subsetRes + map(lambda lst: [inputSet[0]] + lst, subsetRes)
def powerSet2(inputSet):
return reduce(lambda subRes, num: subRes + [[num] + subset for subset in subRes],
inputSet,
[[]])
def powerSet3(inputSet):
size = len(inputSet)
return [[inputSet[i] for i in xrange(size) if (0x1 << i) & num] for num in xrange(2 ** size)]
def main():
assert powerSet([]) == [[]]
assert sorted(powerSet([1])) == [[], [1]]
assert sorted(powerSet([1, 2])) == [[], [1], [1, 2], [2]]
assert sorted(powerSet([1, 2, 3])) == [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
if __name__ == '__main__':
main()
May 3, 2019 [Easy] Running median of a number stream
Question: Compute the running median of a sequence of numbers. That is, given a stream of numbers, print out the median of the list so far on each new element.
Recall that the median of an even-numbered list is the average of the two middle numbers.
For example, given the sequence
[2, 1, 5, 7, 2, 0, 5], your algorithm should print out:
2
1.5
2
3.5
2
2
2
My thoughts: Given a sorted list, the median of a list is either the element in the middle of the list or average of left-max and right-min if we break the original list into left and right part:
* 1, [2], 3
* 1, [2], [3], 4
Notice that, as we get elem from stream 1-by-1, we don’t need to keep the list sorted. If only we could partition the list into two equally large list and mantain the max of the left part and min of right part. We should be good to go.
i,e,
[5, 1, 7] [8 , 20, 10]
^ left-max ^ right-min
A max-heap plus a min-heap will make it a lot easier to mantain the value we are looking for: A max-heap on the left mantaining the largest on left half and a min-heap on the right holding the smallest on right half. And most importantly, we mantain the size of max-heap and min-heap while reading data. (Left and right can at most off by 1).
Python Solution: Link: https://repl.it/@trsong/runningMedianOfStream
from queue import PriorityQueue
# Python doesn't have Max Heap, so we just implement one ourselves
class MaxPriorityQueue(PriorityQueue):
def __init__(self):
PriorityQueue.__init__(self)
def get(self):
return -PriorityQueue.get(self)
def put(self, val):
PriorityQueue.put(self, -val)
def head(queue):
if isinstance(queue, MaxPriorityQueue):
return -queue.queue[0]
else:
return queue.queue[0]
def runningMedianOfStream(stream):
leftMaxHeap = MaxPriorityQueue()
rightMinHeap = PriorityQueue()
result = []
for elem in stream:
# Add elem to the left, when given a smaller-than-left-max number
if leftMaxHeap.empty() or elem < head(leftMaxHeap):
leftMaxHeap.put(elem)
# Add elem to the right, when given a larger-than-right-min number
elif rightMinHeap.empty() or elem > head(rightMinHeap):
rightMinHeap.put(elem)
# Add elem to the left, when given a between-left-max-and-right-min number,
else:
leftMaxHeap.put(elem)
# Re-balance both heaps by transfer elem from larger heap to smaller heap
if len(leftMaxHeap.queue) > len(rightMinHeap.queue) + 1:
rightMinHeap.put(leftMaxHeap.get())
elif len(leftMaxHeap.queue) < len(rightMinHeap.queue) - 1:
leftMaxHeap.put(rightMinHeap.get())
# Calcualte the median base on different situations
leftMaxHeapSize = len(leftMaxHeap.queue)
rightMinHeapSize = len(rightMinHeap.queue)
medium = 0
# Median eqauls (left-max + right-min) / 2
# Be careful for value overflow!
if leftMaxHeapSize == rightMinHeapSize:
midLeft = head(leftMaxHeap)
midRight = head(rightMinHeap)
diff = midRight - midLeft
if diff % 2 == 0:
medium = midLeft + diff / 2
else:
medium = midLeft + diff / 2.0
# Median is left-max
elif leftMaxHeapSize > rightMinHeapSize:
medium = head(leftMaxHeap)
# Median is right-min
else:
medium = head(rightMinHeap)
result.append(medium)
return result
def main():
assert runningMedianOfStream([2, 1, 5, 7, 2, 0, 5]) == [2, 1.5, 2, 3.5, 2, 2, 2]
assert runningMedianOfStream([1, 1, 1, 1, 1, 1]) == [1, 1, 1, 1, 1, 1]
assert runningMedianOfStream([0, 1, 1, 0, 0]) == [0, 0.5, 1, 0.5, 0]
assert runningMedianOfStream([2, 0, 1]) == [2, 1, 1]
assert runningMedianOfStream([3, 0, 1, 2]) == [3, 1.5, 1, 1.5]
if __name__ == '__main__':
main()
May 2, 2019 [Medium] Remove K-th Last Element from Singly Linked-list
Question: Given a singly linked list and an integer k, remove the kth last element from the list. k is guaranteed to be smaller than the length of the list.
Note:
- The list is very long, so making more than one pass is prohibitively expensive.
- Do this in constant space and in one pass.
My thoughts: Use two pointers, faster one are k position ahead of slower one. Once faster reaches last elem, the 1st from the right. Then slow one should be (k + 1) th to the right. i.e. k + 1 - 1 = k. (fast is k position ahead of slow).
k + 1 (from the right) -> k (from the right) -> k - 1 (from the right) -> .... -> 1 (from the right)
^^^^^ slow is here ^ Fast is here
So in order to remove the k-th last element from the list, we just need to point slow.next to the next of that node: slow.next = slow.next.next
Python Solution: Link: https://repl.it/@trsong/removeKthFromEnd
class ListNode(object):
def __init__(self, x, next=None):
self.val = x
self.next = next
def __eq__(self, other):
return not self and not other or self and other and self.next == other.next
def List(*vals):
dummy = ListNode(-1)
p = dummy
for elem in vals:
p.next = ListNode(elem)
p = p.next
return dummy.next
def removeKthFromEnd(head, k):
fast = head
slow = head
# Having two pointers, faster one are k posisition ahead of slower one
for i in xrange(k):
fast = fast.next
# Faster pointer initially starts at position 0, and after k shift, it's null, that means, k is the length of the list.
# So we should remove the first element from the list
if not fast:
return head.next
# Now move fast all the way until the last element in the list
# If fast == last elem, then slow should be last k + 1 element.
# Becasue fast is always k position ahead of slow. (k+1 - 1 == k)
while fast and fast.next:
fast = fast.next
slow = slow.next
# Remove the k-th last elem from the list
slow.next = slow.next.next
return head
def main():
assert removeKthFromEnd(List(1), 1) == List()
assert removeKthFromEnd(List(1, 2), 1) == List(1)
assert removeKthFromEnd(List(1, 2, 3), 1) == List(1, 2)
assert removeKthFromEnd(List(1, 2, 3), 2) == List(1, 3)
assert removeKthFromEnd(List(1, 2, 3), 3) == List(2, 3)
if __name__ == '__main__':
main()
May 1, 2019 [Easy] Balanced Brackets
Question: Given a string of round, curly, and square open and closing brackets, return whether the brackets are balanced (well-formed). For example, given the string “([])”, you should return true. Given the string “([)]” or “((()”, you should return false.
My thoughts: Whenever there is an open bracket, there should be a corresponding close bracket. Likewise, whenver we encounter a close bracket that does not match corresponding open braket, such string is not valid.
So the idea is to iterate through the string, store all the open bracket, and whenever we see a close bracket we check and see if it matches the most rent open breaket we stored early. The data structure, Stack, staisfies all of our requirements.
Python Solution: Link: https://repl.it/@trsong/isBalancedBrackets
def isBalancedBrackets(input):
if not input:
return True
stack = []
lookup = {'(':')', '[':']', '{':'}'}
for char in input:
# Push open bracket to stack
if char in lookup:
stack.append(char)
# Pop open bracket and check if it matches corresponding close bracket
elif stack and char == lookup[stack[-1]]:
stack.pop()
# Short-circuit if open bracket not matches the counterpart
else:
return False
# All char should be processed and nothing should remain in the stack
return not stack
def main():
assert isBalancedBrackets("")
assert not isBalancedBrackets(")")
assert not isBalancedBrackets("(")
assert not isBalancedBrackets("(]")
assert not isBalancedBrackets("[}")
assert not isBalancedBrackets("((]]")
assert not isBalancedBrackets("(][)")
assert isBalancedBrackets("(([]))")
assert isBalancedBrackets("[]{}()")
assert not isBalancedBrackets("())))")
assert isBalancedBrackets("[](())")
if __name__ == '__main__':
main()
Apr 30, 2019 [Medium] Second Largest in BST
Question: Given the root to a binary search tree, find the second largest node in the tree.
My thoughts: Recall the way we figure out the largest element in BST: we go all the way to the right until not possible. So the second largest element must be on the left of largest element. We have two possibilities here:
- Either it’s the parent of rightmost element, if there is no child underneath
- Or it’s the rightmost element in left subtree of the rightmost element.
case 1: parent
1
\
[2]
\
3
case 2: rightmost of left subtree of rightmost
1
\
4
/
2
\
[3]
Python solution: Link: https://repl.it/@trsong/secondLargestInBST
class TreeNode(object):
def __init__(self, x, left=None, right=None):
self.val = x
self.left = left
self.right = right
def secondLargestInBST(node):
if node is None:
return None
# Go all the way to the right until not possible
# Store the second largest on the way
secondLargest = None
current = node
while current.right:
secondLargest = current
current = current.right
# At the rightmost element now and there exists no element between secondLargest and rightmost element
# We have second largest already
if current.left is None:
return secondLargest
# Go left and all the way to the right and the rightmost element shall be the second largest
secondLargest = current.left
current = current.left
while current:
secondLargest = current
current = current.right
return secondLargest
def main():
emptyTree = None
oneElementTree = TreeNode(1)
leftHeavyTree1 = TreeNode(2, TreeNode(1))
leftHeavyTree2 = TreeNode(3, TreeNode(1, right=TreeNode(2)))
rightHeavyTree1 = TreeNode(1, right=TreeNode(2))
rightHeavyTree2 = TreeNode(1, right=TreeNode(3, TreeNode(2)))
balanceTree1 = TreeNode(2, TreeNode(1), TreeNode(3))
balanceTree2 = TreeNode(6, TreeNode(5), TreeNode(7))
balanceTree3 = TreeNode(4, balanceTree1, balanceTree2)
sampleCase1 = TreeNode(1, right=TreeNode(2, right=TreeNode(3)))
sampleCase2 = TreeNode(1, right=TreeNode(4, left=TreeNode(2, right=TreeNode(3))))
assert secondLargestInBST(emptyTree) is None
assert secondLargestInBST(oneElementTree) is None
assert secondLargestInBST(leftHeavyTree1).val == 1
assert secondLargestInBST(leftHeavyTree2).val == 2
assert secondLargestInBST(rightHeavyTree1).val == 1
assert secondLargestInBST(rightHeavyTree2).val == 2
assert secondLargestInBST(balanceTree1).val == 2
assert secondLargestInBST(balanceTree3).val == 6
assert secondLargestInBST(sampleCase1).val == 2
assert secondLargestInBST(sampleCase2).val == 3
if __name__ == '__main__':
main()